题目内容
12．
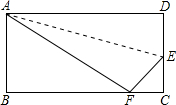如图，在矩形ABCD中，已知AB=6cm，BC=10cm，折叠矩形的一边AD，使点D落在BC边上的点F处，折痕为AE，求CE的长．
分析 根据翻折的性质，先在RT△ABF中求出BF，进而得出FC的长，然后设CE=x，EF=8-x，从而在RT△CFE中应用勾股定理可解出x的值，即能得出CE的长度．
解答 解：由翻折的性质可得：AD=AF=BC=10cm，
在Rt△ABF中可得：BF=$\sqrt{A{F}^{2}-A{B}^{2}}$=8cm，
∴FC=BC-BF=2cm，
设CE=x，EF=DE=6-x，则在Rt△ECF中，
EF2=EC2+CF2，即x2+4=（6-x）2，
解可得x=$\frac{8}{3}$cm．
点评 本题主要通过折叠变换考查了学生的逻辑思维能力，解决本题的关键是结合图形根据翻折的性质得到一些相等的线段，然后灵活运用勾股定理进行解答．
练习册系列答案
红果子三级测试卷系列答案
课堂练加测系列答案
相关题目
7．
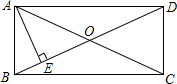如图，在矩形ABCD中，AE⊥BD于E，∠DAE=3∠BAE，则∠EAC为（ ）
如图，在矩形ABCD中，AE⊥BD于E，∠DAE=3∠BAE，则∠EAC为（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 75° |
如图，在?ABCD中，E是AD边上的中点，连接BE并延长与CD的延长线交于点F．证明：AB=DF．
1．
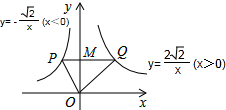函数y=-$\frac{\sqrt{2}}{x}$（x＜0）和y=$\frac{2\sqrt{2}}{x}$（x＞0）的图象如图所示，O为坐标原点，M是y轴正半轴上任意一点，过点M作PQ∥x轴，分别与图中的函数图象相交于P、Q两点，连接OP、OQ，则△OPQ的面积为（ ）
函数y=-$\frac{\sqrt{2}}{x}$（x＜0）和y=$\frac{2\sqrt{2}}{x}$（x＞0）的图象如图所示，O为坐标原点，M是y轴正半轴上任意一点，过点M作PQ∥x轴，分别与图中的函数图象相交于P、Q两点，连接OP、OQ，则△OPQ的面积为（ ）| A． | $\sqrt{2}$ | B． | $\frac{3}{2}\sqrt{2}$ | C． | 2$\sqrt{2}$ | D． | $\frac{5}{2}\sqrt{2}$ |