题目内容
 如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,则tan∠EAF的值=
如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,则tan∠EAF的值=考点:翻折变换(折叠问题)
专题:计算题
分析:先根据矩形的性质得CD=AB=8,AD=BC=10,再根据折叠的性质得AF=AD=10,DE=EF,∠AFE=∠D=90°,在Rt△ABF中,利用勾股定理计算出BF=6,则FC=BC-BF=4,设EF=x,则DE=x,CE=CD-DE=8-x,在Rt△CEF中,根据勾股定理得到42+(8-x)2=x2,解得x=5,即EF=5,然后在Rt△AEF中根据正切的定义求解.
解答:解:∵四边形ABCD为矩形,
∴CD=AB=8,AD=BC=10,
∵折叠矩形ABCD的一边AD,使点D落在BC边的点F处,
∴AF=AD=10,DE=EF,∠AFE=∠D=90°,
在Rt△ABF中,BF=
=6,
∴FC=BC-BF=4,
设EF=x,则DE=x,CE=CD-DE=8-x,
在Rt△CEF中,
∵CF2+CE2=EF2,
∴42+(8-x)2=x2,解得x=5,
即EF=5,
在Rt△AEF中,tan∠EAF=
=
=
.
故答案为:
.
∴CD=AB=8,AD=BC=10,
∵折叠矩形ABCD的一边AD,使点D落在BC边的点F处,
∴AF=AD=10,DE=EF,∠AFE=∠D=90°,
在Rt△ABF中,BF=
| AF2-AB2 |
∴FC=BC-BF=4,
设EF=x,则DE=x,CE=CD-DE=8-x,
在Rt△CEF中,
∵CF2+CE2=EF2,
∴42+(8-x)2=x2,解得x=5,
即EF=5,
在Rt△AEF中,tan∠EAF=
| EF |
| AF |
| 5 |
| 10 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质和勾股定理.

练习册系列答案
相关题目
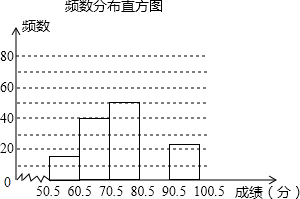 某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分100分)作样本进行统计分析,请根据尚未完成的频率分布表和频数分布直方图,解答下列问题:
某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分100分)作样本进行统计分析,请根据尚未完成的频率分布表和频数分布直方图,解答下列问题: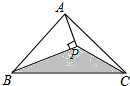 如图,△ABC的面积为4cm2,BP平分∠ABC,且AP⊥BP于P,则△PBC的面积为
如图,△ABC的面积为4cm2,BP平分∠ABC,且AP⊥BP于P,则△PBC的面积为 =0,
=0, =-5,
=-5, =12,
=12, =
= 如图,⊙O的两条弦AB、CD相交于点P,∠D=30°,∠APD=80°,则∠C=
如图,⊙O的两条弦AB、CD相交于点P,∠D=30°,∠APD=80°,则∠C=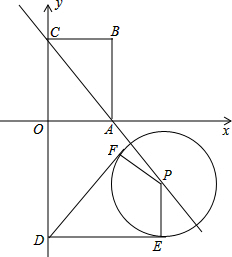 已知如图平面直角坐标系中,点O是坐标原点,矩形ABCO是顶点坐标分别为A(3,0)、B(3,4)、C(0,4).点D在y轴上,且点D的坐标为(0,-5),点P是直线AC上的一动点.
已知如图平面直角坐标系中,点O是坐标原点,矩形ABCO是顶点坐标分别为A(3,0)、B(3,4)、C(0,4).点D在y轴上,且点D的坐标为(0,-5),点P是直线AC上的一动点.