题目内容
 如图,是两块边长分别为a、b的黑色正方形瓷砖和两块白色的长方形瓷砖拼成的无缝图案.
如图,是两块边长分别为a、b的黑色正方形瓷砖和两块白色的长方形瓷砖拼成的无缝图案.(1)根据图中条件,用两种方法表示两个阴影图形的面积的和(只需表示,不必化简);
(2)由(1),你能得到怎样的等量关系?请用等式表示;
(3)如果图中的a,b(a>b)满足a2+b2=53,ab=14,求:a-b.
考点:完全平方公式的几何背景
专题:
分析:(1)利用各图形的面积求解即可,
(2)由(1)中的面积可得等量关系式,
(3)利用完全平方公式求解即可.
(2)由(1)中的面积可得等量关系式,
(3)利用完全平方公式求解即可.
解答:解:(1)两个阴影图形的面积和可表示为:a2+b2或 (a+b)2-2ab,
(2)a2+b2或 (a+b)2-2ab,
(3)∵a2+b2=53,ab=14,
∴(a-b)2=a2+b2-2ab=25,
∴a-b=±5,
又∵a>b>0,
∴a-b=5.
(2)a2+b2或 (a+b)2-2ab,
(3)∵a2+b2=53,ab=14,
∴(a-b)2=a2+b2-2ab=25,
∴a-b=±5,
又∵a>b>0,
∴a-b=5.
点评:本题主要考查了完全平方公式的几何背景,解题的关键是明确四块图形的面积.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
一个三角形任意一边上的高都是这边上的中线,则对这个三角形最准确的判断是( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
△ABC中,a、b、c分别是∠A、∠B、∠C的对边,如果a2+b2=c2,那么下列结论不正确的是( )
| A、c•sinA=a |
| B、c•cosB=b |
| C、b•tanA=a |
| D、a•tanB=b |
 有理数a、b在数轴上的对应的点的位置如图所示,则( )
有理数a、b在数轴上的对应的点的位置如图所示,则( )| A、a+b<0 | B、b-a<0 |
| C、ab>0 | D、a÷b>0 |
在比例尺为1:50000的地图上,量得A、B两地的距离为15厘米,则A、B两地的实际距离是( )
| A、5千米 | B、15千米 |
| C、7.5千米 | D、9千米 |
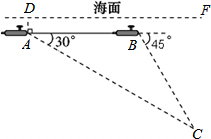 如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1464米到B点处测得正前方C点处的俯角为45°.则海底C点处距离海面DF的深度为
如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1464米到B点处测得正前方C点处的俯角为45°.则海底C点处距离海面DF的深度为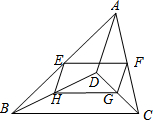 如图,D是△ABC内一点,BD⊥CD,AD=12,BD=8,CD=6,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是( )
如图,D是△ABC内一点,BD⊥CD,AD=12,BD=8,CD=6,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是( )