题目内容
△ABC中,∠A:∠B:∠C=1:2:3,CD⊥AB于点D,若BC=a,则AD等于( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:含30度角的直角三角形
专题:
分析:首先由已知△ABC中,∠A:∠B:∠C=l:2:3,求出∠A=30°,∠B=60°,∠ACB=90°,由CD⊥AB,在Rt△BCD利用三角函数求得BD的长,即可求得AD的长.
解答:解:已知△ABC中,∠A:∠B:∠C=l:2:3,
∴∠A=180×
=30°,
∠B=180°×
=60°,
∠ACB=180°×
=90°,
又∵CD⊥AB,
∴在Rt△ABC中,AB=2BC=2a,
∵在直角△BCD中,∠BCD=30°.
∴BD=AB•cosB=
BC=
a,
则BD=2a-
a=
a.
故选C.

∴∠A=180×
| 1 |
| 1+2+3 |
∠B=180°×
| 2 |
| 1+2+3 |
∠ACB=180°×
| 3 |
| 1+2+3 |
又∵CD⊥AB,
∴在Rt△ABC中,AB=2BC=2a,
∵在直角△BCD中,∠BCD=30°.
∴BD=AB•cosB=
| 1 |
| 2 |
| 1 |
| 2 |
则BD=2a-
| 1 |
| 2 |
| 3 |
| 2 |
故选C.
点评:本题考查了直角三角形的性质,直角三角形中30°的锐角所求的直角边等于斜边的一半.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
已知关于x的方程3x=9与-x=1-k的解相同,则k的值为( )
| A、2 | B、-2 | C、4 | D、-4 |
一个三角形任意一边上的高都是这边上的中线,则对这个三角形最准确的判断是( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
 如图,在△ABC中,AB=8,AC=6,∠BAC=90°,AD是BC边上的高,D为垂足,将△ABC折叠使点A与点D重合,则折痕EF的长为
如图,在△ABC中,AB=8,AC=6,∠BAC=90°,AD是BC边上的高,D为垂足,将△ABC折叠使点A与点D重合,则折痕EF的长为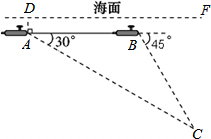 如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1464米到B点处测得正前方C点处的俯角为45°.则海底C点处距离海面DF的深度为
如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1464米到B点处测得正前方C点处的俯角为45°.则海底C点处距离海面DF的深度为 如图所示,已知AB∥CD,∠1=∠2,试说明∠E=∠F,写出你的推理过程.
如图所示,已知AB∥CD,∠1=∠2,试说明∠E=∠F,写出你的推理过程.