题目内容
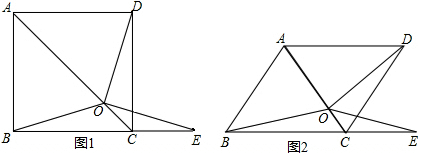
17.如图1,在正方形ABCD中,O是对角线AC上一点,点E在BC的延长线上,且OE=OB.(1)求证:△OBC≌△ODC.
(2)求证:∠DOE=∠ABC.
(3)把正方形ABCD改为菱形,其他条件不变(如图2),若∠ABC=52°,求∠DOE的度数.
分析 (1)根据正方形的性质得出∠BCO=∠DCO,再根据全等三角形的判定证明即可;
(2)根据全等三角形的性质得出∠CBO=∠CDO,再利用对顶角相等和平行线性质证明即可.
(3)借助(1)(2)的方法可求得∠DOE=∠ABC=52°.
解答 解:(1)∵AC是正方形ABCD的对角线,
∴BC=DC,∠BCA=∠DCA,
在△BCO和△DCO中,$\left\{\begin{array}{l}{BC=DC}\\{∠BCO=∠DCO}\\{CO=CO}\end{array}\right.$,
∴△BCO≌△DCO(SAS);
(2)如图1,
由(1)知,△BCO≌△DCO,
∴∠CBO=∠CDO,
∵OE=OB,
∴∠CBO=∠E,
∴∠CDO=∠E,
∵∠DFO=∠EFC(对顶角相等),
∴180°-∠DFO-∠CDP=180°-∠EFC-∠E,
即∠DOE=∠DCE,
∵AB∥CD,
∴∠DCE=∠ABC,
∴∠DOE=∠ABC.
(3)如图2, ∵AC是菱形ABCD的对角线,
∵AC是菱形ABCD的对角线,
∴BC=DC,∠BCA=∠DCA,
在△BCO和△DCO中,$\left\{\begin{array}{l}{BC=DC}\\{∠BCO=∠DCO}\\{CO=CO}\end{array}\right.$,
∴△BCO≌△DCO(SAS);
∴∠CBO=∠CDO,
∵OE=OB,
∴∠CBO=∠E,
∴∠CDO=∠E,
∵∠DFO=∠EFC(对顶角相等),
∴180°-∠DFO-∠CDP=180°-∠EFC-∠E,
即∠DOE=∠DCE,
∵AB∥CD,
∴∠DCE=∠ABC,
∴∠DOE=∠ABC=52°.
点评 此题是四边形综合题,主要考查了正方形的性质,菱形的性质,全等三角形的判定和性质,平行线的性质,三角形的内角和,解本题的关键是判断出△BCO≌△DCO,是一道中等难度的中考常考题.

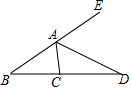 AD是∠CAE的平分线,∠B=35°,∠DAE=60°,则∠ACD=( )
AD是∠CAE的平分线,∠B=35°,∠DAE=60°,则∠ACD=( )| A. | 25° | B. | 60° | C. | 85° | D. | 95° |
| A. | 互为倒数 | B. | 互为相反数 | C. | 相等 | D. | 互为负倒数 |
 如图,∠MON=30°,点A、B分别在射线OM,ON上,且AB=6,∠AB0≤90°,在线段OB上取点C,使得∠CAB=∠MON.
如图,∠MON=30°,点A、B分别在射线OM,ON上,且AB=6,∠AB0≤90°,在线段OB上取点C,使得∠CAB=∠MON.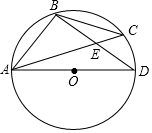 已知⊙O上两个定点A、B和两个动点C、D,AC与BD交于点E.
已知⊙O上两个定点A、B和两个动点C、D,AC与BD交于点E.
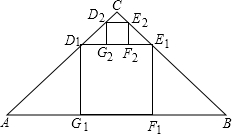 如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,在Rt△ABC内部作正方形D1E1F1G1,其中点D1,E1分别在AC,BC边上,边F1G1在BC上,它的面积记作S1;按同样的方法在△CD1E1内部作正方形D2E2F2G2,它的面积记作S2,S2=$\frac{8}{{3}^{4}}$,…,照此规律作下去,正方形DnEnFnGn的面积Sn=$\frac{8}{{3}^{2n}}$.
如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,在Rt△ABC内部作正方形D1E1F1G1,其中点D1,E1分别在AC,BC边上,边F1G1在BC上,它的面积记作S1;按同样的方法在△CD1E1内部作正方形D2E2F2G2,它的面积记作S2,S2=$\frac{8}{{3}^{4}}$,…,照此规律作下去,正方形DnEnFnGn的面积Sn=$\frac{8}{{3}^{2n}}$.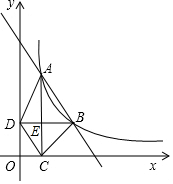 如图,在平面直角坐标系中,函数y=$\frac{k}{x}$(x>0,k是常数)的图象经过A(2,6),B(m,n),其中m>2.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,AC与BD交于点E,连结AD,DC,CB.
如图,在平面直角坐标系中,函数y=$\frac{k}{x}$(x>0,k是常数)的图象经过A(2,6),B(m,n),其中m>2.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,AC与BD交于点E,连结AD,DC,CB.