题目内容
2.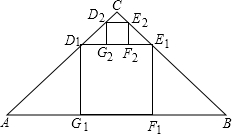 如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,在Rt△ABC内部作正方形D1E1F1G1,其中点D1,E1分别在AC,BC边上,边F1G1在BC上,它的面积记作S1;按同样的方法在△CD1E1内部作正方形D2E2F2G2,它的面积记作S2,S2=$\frac{8}{{3}^{4}}$,…,照此规律作下去,正方形DnEnFnGn的面积Sn=$\frac{8}{{3}^{2n}}$.
如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,在Rt△ABC内部作正方形D1E1F1G1,其中点D1,E1分别在AC,BC边上,边F1G1在BC上,它的面积记作S1;按同样的方法在△CD1E1内部作正方形D2E2F2G2,它的面积记作S2,S2=$\frac{8}{{3}^{4}}$,…,照此规律作下去,正方形DnEnFnGn的面积Sn=$\frac{8}{{3}^{2n}}$.
分析 易知AB=3G1F1,G1F1=3G2F2,求出第一个、第二个正方形的面积,探究规律后即可解决问题.
解答 解:∵CA=CB,∴∠C=90°,
∴∠A=∠B=45°,
∵正方形D1E1F1G1,易知AB=3G1F1,G1F1=3G2F2,
∴正方形D1E1F1G1的边长为$\frac{2\sqrt{2}}{3}$,面积为$\frac{8}{9}$=$\frac{8}{{3}^{2}}$,
正方形D2E2F2G2,的边长为$\frac{2\sqrt{2}}{9}$,面积为$\frac{8}{{3}^{4}}$,
…,
正方形DnEnFnGn的面积Sn=$\frac{8}{{3}^{2n}}$,
故答案分别为$\frac{8}{{3}^{4}}$,$\frac{8}{{3}^{2n}}$.
点评 本题考查等腰直角三角形的性质、正方形的性质等知识,解题的关键是学会探究规律、利用规律解决问题,属于中考常考题型.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
12.若分式$\frac{2xy}{x-3y}$中的x,y的值都变为原来的5倍,则此分式的值( )
| A. | 不变 | B. | 是原来的5倍 | C. | 是原来的$\frac{1}{5}$ | D. | 是原来的$\frac{1}{10}$ |
13.若|a|=$\sqrt{3}$,则a=( )
| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | ±$\sqrt{3}$ | D. | 3 |
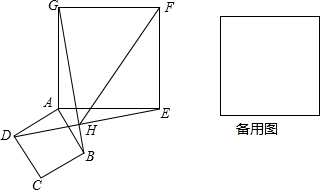 如图,已知正方形ABCD、AEFG边长分别为$\sqrt{2}$cm、2cm,将正方形ABCD绕点A旋转,连接BG、DE相交于点H.
如图,已知正方形ABCD、AEFG边长分别为$\sqrt{2}$cm、2cm,将正方形ABCD绕点A旋转,连接BG、DE相交于点H.