题目内容
11.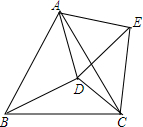 如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,则∠CDE的正弦值为$\frac{3\sqrt{7}}{8}$.
如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,则∠CDE的正弦值为$\frac{3\sqrt{7}}{8}$.
分析 先根据等边三角形的性质得AB=AC,∠BAC=60°,再根据旋转的性质得∠DAE=∠BAC=60°,AD=AE,CE=BD=6,于是可判断△ADE为等边三角形,所以DE=AD=5,作CH⊥DE于H,如图,设DH=x,则HE=DE-DH=5-x
,利用勾股定理得到42-x2=62-(5-x)2,解得x=$\frac{1}{2}$,则可计算出CH=$\frac{3\sqrt{7}}{2}$,然后根据正弦的定义求解.
解答 解:∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°,
∵△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,
∴∠DAE=∠BAC=60°,AD=AE,CE=BD=6,
∵△ADE为等边三角形,
∴DE=AD=5,
作CH⊥DE于H,如图,设DH=x,则HE=DE-DH=5-x
在Rt△CDH中,CH2=CD2-DH2=42-x2,
在Rt△CEH中,CH2=CE2-EH2=62-(5-x)2,
∴42-x2=62-(5-x)2,解得x=$\frac{1}{2}$,
在Rt△CDH中,CH=$\sqrt{{4}^{2}-(\frac{1}{2})^{2}}$=$\frac{3\sqrt{7}}{2}$,
∴sin∠CDH=$\frac{CH}{CD}$=$\frac{\frac{3\sqrt{7}}{2}}{4}$=$\frac{3\sqrt{7}}{8}$,
即sin∠CDH=$\frac{3\sqrt{7}}{8}$.
故答案为$\frac{3\sqrt{7}}{8}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.解决本题的关键是求C点到DE的距离.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
2.下列各点中,在函数y=$\frac{2}{x}$的图象上的点是( )
| A. | (1,0.5) | B. | (2,-1) | C. | (-1,-2) | D. | (-2,1) |
 如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,求△DCE的面积.
如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,求△DCE的面积. 如图,B在AE上,C在BG上,四边形ABCD和四边形BEFG都是正方形,连结AG和EC.
如图,B在AE上,C在BG上,四边形ABCD和四边形BEFG都是正方形,连结AG和EC.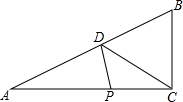 在Rt△ABC中,∠ACB=90°,点D是斜边AB上的中点,AC=6cm,BC=4cm,一动点P从点A出发,沿A→C→B的路线以1cm/s的速度移动.设△APD的面积为y(cm2),则y关于点P的运动时间x(s)的函数图象大致是( )
在Rt△ABC中,∠ACB=90°,点D是斜边AB上的中点,AC=6cm,BC=4cm,一动点P从点A出发,沿A→C→B的路线以1cm/s的速度移动.设△APD的面积为y(cm2),则y关于点P的运动时间x(s)的函数图象大致是( )



 一个几何体由12个大小相同的小立方体搭成,从上面看到的这个几何体的形状图如图所示,若小正方形中的数字表示在该位置小立方块的个数,则从正面看,一共能看到8个小立方块(被遮挡的不计).
一个几何体由12个大小相同的小立方体搭成,从上面看到的这个几何体的形状图如图所示,若小正方形中的数字表示在该位置小立方块的个数,则从正面看,一共能看到8个小立方块(被遮挡的不计).