题目内容
9.已知等腰△APP1、△BPP2中,AP=AP1,BP=BP2,A、P、B在同一条直线上,且∠A=∠B=α.(1)如图①,当α=90°时,求∠P1PP2的度数;
(2)如图②,当点P2在AP1的延长线上时,∠P2PP1的度数(用含α的代数式表示).
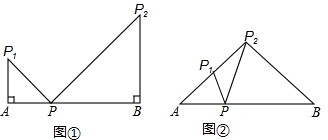
分析 (1)根据等腰直角三角形的性质进行计算即可;
(2)根据等腰三角形的性质和三角形内角和定理进行解答即可.
解答 解:(1)∵AP=AP1,BP=BP2,α=90°,
∴△APP1和△BPP2都是等腰直角三角形,
∴APP1=BPP2=45°,
∴∠P1PP2=90°,
答:∠P1PP2的度数是90°;
(2)∵AP=AP1,BP=BP2,
∴APP1=BPP2=90°-$\frac{α}{2}$,
∴∠P1PP2=180°-(90°-$\frac{α}{2}$)=α,
答:∠P2PP1的度数为α.
点评 本题考查的是等腰直角三角形的知识,掌握等腰直角三角形两个锐角都是45°、三角形内角和等于180°是解题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
17.某年级380名师生秋游,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表.
(1)设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;
(2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元?
| 甲种客车 | 乙种客车 | |
| 载客量(座/辆) | 60 | 45 |
| 租金(元/辆) | 550 | 450 |
(2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元?
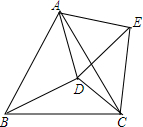 如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,则∠CDE的正弦值为$\frac{3\sqrt{7}}{8}$.
如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,则∠CDE的正弦值为$\frac{3\sqrt{7}}{8}$.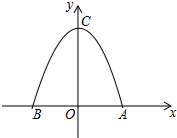 某菜农搭建了一个横截面为抛物线的大棚,建立如图所示的直角坐标系后,抛物线的表达式为y=-$\frac{1}{2}$x2+2.
某菜农搭建了一个横截面为抛物线的大棚,建立如图所示的直角坐标系后,抛物线的表达式为y=-$\frac{1}{2}$x2+2. 如图,AF是△ABC的高,点D、E分别在AB、AC上,且DE∥BC,DE交AF于点G.设AD=10,AB=30,AC=24,GF=12.
如图,AF是△ABC的高,点D、E分别在AB、AC上,且DE∥BC,DE交AF于点G.设AD=10,AB=30,AC=24,GF=12.