题目内容
4. 如图,B在AE上,C在BG上,四边形ABCD和四边形BEFG都是正方形,连结AG和EC.
如图,B在AE上,C在BG上,四边形ABCD和四边形BEFG都是正方形,连结AG和EC.(1)求证:△ABG≌△CBE;
(2)求证:AG⊥EC.
分析 (1)由正方形的性质得出AB=BC,∠ABG=∠CBE=90°,BG=BE,由SAS证明△ABG≌△CBE即可;
(2)延长EC交AG于M,由全等三角形的性质得出∠G=∠E,由角的互余关系和对顶角相等得出∠G+∠GCM=90°,因此∠GMC=90°,即可得出结论.
解答 (1)证明:∵四边形ABCD和四边形BEFG都是正方形,
∴AB=BC,∠ABG=∠CBE=90°,BG=BE,
在△ABG和△CBE中,$\left\{\begin{array}{l}{AB=BC}&{\;}\\{∠ABG=∠CBE}&{\;}\\{BG=BE}&{\;}\end{array}\right.$,
∴△ABG≌△CBE(SAS);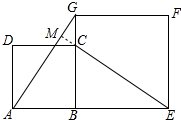
(2)证明:延长EC交AG于M,如图所示:
由(1)得:△ABG≌△CBE,
∴∠G=∠E,
∵∠E+∠BCE=90°,∠GCM=∠BCE,
∴∠G+∠GCM=90°,
∴∠GMC=90°,
∴AG⊥EC.
点评 本题考查了全等三角形的判定与性质、正方形的性质、对顶角相等;熟练掌握正方形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
7.若△ABC与△DEF相似,相似比为2:3,则这两个三角形的面积比为( )
| A. | 2:3 | B. | 3:2 | C. | 4:9 | D. | 9:4 |
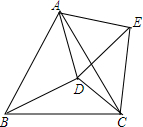 如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,则∠CDE的正弦值为$\frac{3\sqrt{7}}{8}$.
如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,则∠CDE的正弦值为$\frac{3\sqrt{7}}{8}$.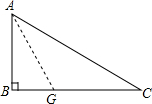 如图,已知直角△ABC中,∠B=90°,AB=6cm,BC=8cm,把AB沿AG折叠,使B点恰好落在AC上,求折痕AG的长.
如图,已知直角△ABC中,∠B=90°,AB=6cm,BC=8cm,把AB沿AG折叠,使B点恰好落在AC上,求折痕AG的长.