Question

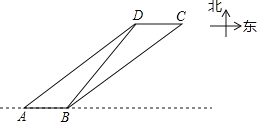
【题目】如图为某海域示意图，其中灯塔D的正东方向有一岛屿C．一艘快艇以每小时20nmile的速度向正东方向航行，到达A处时得灯塔D在东北方向上，继续航行0.3h，到达B处时测得灯塔D在北偏东30°方向上，同时测得岛屿C恰好在B处的东北方向上，此时快艇与岛屿C的距离是多少？（结果精确到1nmile．参考数据：≈1.41，≈1.73，≈2.45）

Answer 1

【答案】此时快艇与岛屿C的距离是20nmile．

【解析】

过点D作DE⊥AB于点E，过点C作CF⊥AB于点F，由DE∥CF，DC∥EF，∠CFE=90°可得出四边形CDEF为矩形，设DE=x nmile，则AE=x （nmile），BE=x（nmile），由AB=6 nmile，可得出关于x的一元一次方程，解之即可得出x的值，再在Rt△CBF中，通过解直角三角形可求出BC的长．

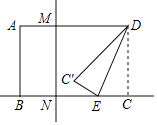
解：过点D作DE⊥AB于点E，过点C作CF⊥AB于点F，如图所示．

则DE∥CF，∠DEA＝∠CFA＝90°．

∵DC∥EF，

∴四边形CDEF为平行四边形．

又∵∠CFE＝90°，

∴CDEF为矩形，

∴CF＝DE．

根据题意，得：∠DAB＝45°，∠DBE＝60°，∠CBF＝45°．

设DE＝x（nmile），

在Rt△DEA中，∵tan∠DAB＝，

∴AE＝＝x（nmile）．

在Rt△DEB中，∵tan∠DBE＝，

∴BE＝＝x（nmile）．

∵AB＝20×0.3＝6（nmile），AE﹣BE＝AB，

∴x﹣x＝6，解得：x＝9+3，

∴CF＝DE＝（9+3）nmile．

在Rt△CBF中，sin∠CBF＝，

∴BC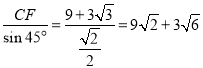＝≈20（nmile）．

答：此时快艇与岛屿C的距离是20nmile．