Question

【题目】如图，在矩形ABCD中，AB＝5，BC＝6，点M，N分别在AD，BC上，且AM＝AD，BN＝BC，E为直线BC上一动点，连接DE，将△DCE沿DE所在直线翻折得到△DC′E，当点C′恰好落在直线MN上时，CE的长为___．

Answer 1

【答案】或10．

【解析】

由矩形的性质得到DC=AB=5，∠A=90°，AD=BC=6，根据已知条件得到AM=BN，推出四边形ABNM的矩形，得到∠NMA=∠NMD=90°，MN=AB=5，根据折叠的性质得到DC′=DC=5，C′E=CE，根据勾股定理得到C′M=，根据矩形的判定和性质得到CN=DM=4，∠CNM=90°，再由勾股定理即可得到结论．

解：∵四边形ABCD是矩形，

∴DC＝AB＝5，∠A＝90°，AD＝BC＝6，

∵AM＝AD＝2，BN＝BC＝2，

∴AM＝BN，

∵AM∥BN，

∴四边形ABNM的矩形，

∴∠NMA＝∠NMD＝90°，MN＝AB＝5，

∵将△DCE沿DE所在直线翻折得到△DC′E，

∴DC′＝DC＝5，C′E＝CE，

∵AM＝2，

∴DM＝AD﹣AM＝6﹣2＝4，

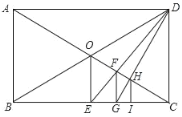
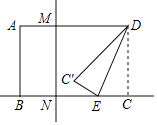
如图1，

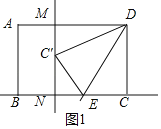
在Rt△C′MD中，C′M＝，

∴C′N＝MN﹣C′M＝5﹣3＝2，

∵∠CDM＝∠DCN＝∠NMD＝90°，

∴四边形CDMN是矩形，

∴CN＝DM＝4，∠CNM＝90°，

NE＝CN﹣CE＝4﹣CE，

在Rt△C′NE中，∵NE2+C′N2＝C′E2，

∴（4﹣CE）2+22＝CE2，

解得：CE＝．

如图2，

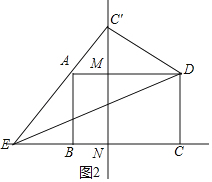
在Rt△C′MD中，C′M＝，

∴C′N＝MN+C′M＝5+3＝8，

∵∠CDM＝∠DCN＝∠NMD＝90°，

∴四边形CDMN是矩形，

∴CN＝DM＝4，∠CNM＝∠MNE＝90°，

NE＝CE﹣CN＝CE﹣4，

在Rt△C′NE中，∵NE2+C′N2＝C′E2，

∴（CE﹣4）2+82＝CE2，

解答：CE＝10，

故答案为：或10．