题目内容
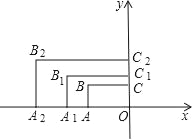
【题目】如图，在平面直角坐标系中，矩形AOCB的两边OA，OC分别在x轴和y轴上，且OA＝2．OC＝1，则矩形AOCB的对称中心的坐标是___；在第二象限内，将矩形AOCB以原点O为位似中心放大为原来的
倍，得到矩形A1OC1B1，再将矩形A1OC1B1以原点O为位似中心放大倍，得到矩形A2OC2B，…，按此规律，则矩形A4OC4B4的对称中心的坐标是___．
【答案】（﹣1，
）， （﹣
，
）．
【解析】
先利用矩形的性质写出B点坐标，则根据线段中点坐标公式可写出矩形AOCB的对称中心的坐标；再利用以原点为位似中心的对应点的坐标之间的关系分别写出B1、B2、B3、B4的坐标，然后矩形A4OC4B4的对称中心的坐标．
解：∵OA=2．OC=1，
∴B（-2，1），
∴矩形AOCB的对称中心的坐标为（-1，
），
∵将矩形AOCB以原点O为位似中心放大为原来的
倍，得到矩形A1OC1B1，
∴B1（-3，），
同理可得B2（-
，
），B3（-
，
），B4（-
，
），
∴矩形A4OC4B4的对称中心的坐标是（﹣，
）．
故答案为：（-1，），（﹣，）．
练习册系列答案
相关题目
