题目内容
【题目】如图,正方形ABCD的边长为2a,E为BC边的中点,![]() 的圆心分别在边AB、CD上,这两段圆弧在正方形内交于点F,则E、F间的距离为 .
的圆心分别在边AB、CD上,这两段圆弧在正方形内交于点F,则E、F间的距离为 .
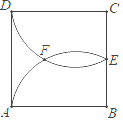
【答案】![]() a.
a.
【解析】
作DE的中垂线交CD于G,则G为![]() 的圆心,H为
的圆心,H为![]() 的圆心,连接EF,GH,交于点O,连接GF,FH,HE,EG,依据勾股定理可得GE=FG=
的圆心,连接EF,GH,交于点O,连接GF,FH,HE,EG,依据勾股定理可得GE=FG=![]() a,根据四边形EGFH是菱形,四边形BCGH是矩形,即可得到Rt△OEG中,OE=
a,根据四边形EGFH是菱形,四边形BCGH是矩形,即可得到Rt△OEG中,OE=![]() a,即可得到EF=
a,即可得到EF=![]() a.
a.
如图,作DE的中垂线交CD于G,则G为![]() 的圆心,同理可得,H为
的圆心,同理可得,H为![]() 的圆心,
的圆心,
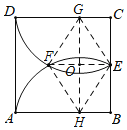
连接EF,GH,交于点O,连接GF,FH,HE,EG,
设GE=GD=x,则CG=2a-x,CE=a,
Rt△CEG中,(2a-x)2+a2=x2,
解得x=![]() a,
a,
∴GE=FG=![]() a,
a,
同理可得,EH=FH=![]() a,
a,
∴四边形EGFH是菱形,四边形BCGH是矩形,
∴GO=![]() BC=a,
BC=a,
∴Rt△OEG中,OE=![]() ,
,
∴EF=![]() a,
a,
故答案为:![]() a.
a.

练习册系列答案
相关题目