题目内容
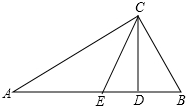
10. 如图,某地下车库的入口处有斜坡CB,它的坡度为i=1:2.4,斜坡CB的长为13米.
如图,某地下车库的入口处有斜坡CB,它的坡度为i=1:2.4,斜坡CB的长为13米.(1)求车库的高度CD;
(2)为了让行车更安全,现将斜坡的坡角改造为14°,求改造后的斜坡AC的长.(结果精确到1米,参考数据:sin14°≈0.24,cos14°≈0.97,tan14°≈0.25)
分析 (1)设CD=x,根据坡度的概念用x表示出BD,根据勾股定理列出方程,解方程即可;
(2)根据正弦的定义列出算式,求出AC.
解答 解:(1)设CD=x,
∵它的坡度为i=1:2.4,
∴BD=2.4x,
由勾股定理得,x2+(2.4x)2=132,
解得,x1═5,x2=-5(不合题意),
答:车库的高度CD为5米;
(2)在Rt△ACD中,
AC=$\frac{CD}{sin14°}$=$\frac{5}{0.24}$≈2.1,
答:改造后的斜坡AC的长约为2.1米.
点评 本题考查的是解直角三角形的应用-坡度坡角问题,掌握坡度的概念、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.计算-2-8的结果是( )
| A. | -6 | B. | -10 | C. | 10 | D. | 6 |
15.如果$\left\{\begin{array}{l}{x=2}\\{y=5}\end{array}\right.$是方程kx-2y=0的一个解,则k等于( )
| A. | 5 | B. | $\frac{8}{5}$ | C. | 6 | D. | -$\frac{8}{3}$ |
20.下列语句是命题是( )
| A. | 画线段AB | B. | 内错角相等 | C. | 请不要讲话 | D. | 对顶角相等吗? |
 如图,Rt△ABC中,∠ACB=90°,∠A=30°,AB=8,CD是斜边AB上的高,CE是中线,DE=2.
如图,Rt△ABC中,∠ACB=90°,∠A=30°,AB=8,CD是斜边AB上的高,CE是中线,DE=2.