题目内容
2.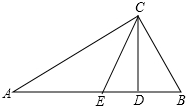 如图,Rt△ABC中,∠ACB=90°,∠A=30°,AB=8,CD是斜边AB上的高,CE是中线,DE=2.
如图,Rt△ABC中,∠ACB=90°,∠A=30°,AB=8,CD是斜边AB上的高,CE是中线,DE=2.
分析 根据直角三角形中30°所对的边是斜边的一半可求得BC的长,再根据直角三角形斜边上的中线等于斜边的一半可得到CE=BE=BC,从而根据可判定△BCE是等边三角形,根据等边三角形的性质不难求得DE的长.
解答 解:∵Rt△ABC中,∠ACB=90°,∠A=30°,AB=8,CD是斜边AB上的高,CE是中线,
∴BC=BE=CE=4,
∴△BCE是等边三角形,
∵CD是斜边AB上的高,
∴CD也是BE边上的中线,
∴ED=$\frac{1}{2}$EB=2.
故答案是:2.
点评 此题主要考查直角三角形斜边上的中线的性质,含30°角的直角三角形的性质及等边三角形的判定与性质的综合运用能力.

练习册系列答案
相关题目
12.下列运算中正确的是( )
| A. | 2a-a=2 | B. | a2+a3=a5 | C. | ab2÷a=b2 | D. | (-2a)3=-6a3 |
13.时钟钟面上的分针的长为1,经过30分,分针在钟面上扫过的面积是( )
| A. | $\frac{1}{2}π$ | B. | $\frac{1}{4}$π | C. | $\frac{1}{8}$π | D. | π |
17.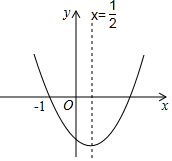 抛物线y=ax2+bx+c的图象如图所示,则一元二次方程ax2+bx+c=0的两根是( )
抛物线y=ax2+bx+c的图象如图所示,则一元二次方程ax2+bx+c=0的两根是( )
 抛物线y=ax2+bx+c的图象如图所示,则一元二次方程ax2+bx+c=0的两根是( )
抛物线y=ax2+bx+c的图象如图所示,则一元二次方程ax2+bx+c=0的两根是( )| A. | x1=-1,x2=$\frac{1}{2}$ | B. | x1=-1,x2=0 | C. | x1=-1,x2=2 | D. | x1=-1,x2=$\frac{3}{2}$ |
14.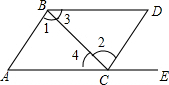 如图所示,点E在AC的延长线上,下列条件中能判断AC∥BD的是( )
如图所示,点E在AC的延长线上,下列条件中能判断AC∥BD的是( )
 如图所示,点E在AC的延长线上,下列条件中能判断AC∥BD的是( )
如图所示,点E在AC的延长线上,下列条件中能判断AC∥BD的是( )| A. | ∠1=∠2 | B. | ∠D+∠ABD=180° | C. | ∠3=∠4 | D. | ∠DCE=∠A |
12. 如图,△ABC≌△DEF,则∠E的度数为( )
如图,△ABC≌△DEF,则∠E的度数为( )
 如图,△ABC≌△DEF,则∠E的度数为( )
如图,△ABC≌△DEF,则∠E的度数为( )| A. | 80° | B. | 40° | C. | 62° | D. | 38° |
 如图,某地下车库的入口处有斜坡CB,它的坡度为i=1:2.4,斜坡CB的长为13米.
如图,某地下车库的入口处有斜坡CB,它的坡度为i=1:2.4,斜坡CB的长为13米.