题目内容
10. 如图,△ABC中,∠C=90°,AB=2AC,D为AB上一点,DE⊥BC于E,且DE=$\frac{1}{2}$BD,BE=AC.若DE+BC=3,求BD的长.
如图,△ABC中,∠C=90°,AB=2AC,D为AB上一点,DE⊥BC于E,且DE=$\frac{1}{2}$BD,BE=AC.若DE+BC=3,求BD的长.
分析 先利用正弦的定义可求出∠B=30°,设DE=x,则BD=2x,BE=$\sqrt{3}$x,所以AC=$\sqrt{3}$x,再在Rt△ACB利用正切的定义可表示出BC=3x,由于DE+BC=3,则x+3x=3,解得x=$\frac{3}{4}$,所以BD=2x=$\frac{3}{2}$.
解答 解:∵∠C=90°,AB=2AC,
∴sinB=$\frac{AC}{AB}$=$\frac{1}{2}$,
∴∠B=30°,
设DE=x,则BD=2x,BE=$\sqrt{3}$x,
所以AC=$\sqrt{3}$x,
∵DE⊥BC,
∴∠ACB=90°,
在Rt△ACB,∵tanB=$\frac{AC}{BC}$,
∴BC=$\frac{\sqrt{3}x}{tan30°}$=3x,
而DE+BC=3,
∴x+3x=3,解得x=$\frac{3}{4}$,
∴BD=2x=$\frac{3}{2}$.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.也考查了解直角三角形.

练习册系列答案
相关题目
5. 如图可以用来反映这样一个实际情况,一艘船从甲地航行到乙地,达到乙地后即返回,这里横坐标表示航行的时间,纵坐标表示船只与甲地的距离,你认为,船只从甲地到乙地航行的速度与返航的速度是否相同?说说理由.
如图可以用来反映这样一个实际情况,一艘船从甲地航行到乙地,达到乙地后即返回,这里横坐标表示航行的时间,纵坐标表示船只与甲地的距离,你认为,船只从甲地到乙地航行的速度与返航的速度是否相同?说说理由.
 如图可以用来反映这样一个实际情况,一艘船从甲地航行到乙地,达到乙地后即返回,这里横坐标表示航行的时间,纵坐标表示船只与甲地的距离,你认为,船只从甲地到乙地航行的速度与返航的速度是否相同?说说理由.
如图可以用来反映这样一个实际情况,一艘船从甲地航行到乙地,达到乙地后即返回,这里横坐标表示航行的时间,纵坐标表示船只与甲地的距离,你认为,船只从甲地到乙地航行的速度与返航的速度是否相同?说说理由.
15.-π的相反数是( )
| A. | -π | B. | 3.14 | C. | -3.14 | D. | 以上不对 |
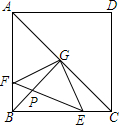 如图,正方形ABCD,点G为AC的中点,作∠EGF=90°,点E在BC上,点F在AB上,EF、BG的交点为P,求证:AF2+CE2=2GP•BG.
如图,正方形ABCD,点G为AC的中点,作∠EGF=90°,点E在BC上,点F在AB上,EF、BG的交点为P,求证:AF2+CE2=2GP•BG. 已知在△ABC中,∠BAD=∠CAD,∠B=∠FAC,点F为BC延长线上的一点,且FE平分∠AFD交AB于点E,试判断EF与AD之间的位置关系,并证明.
已知在△ABC中,∠BAD=∠CAD,∠B=∠FAC,点F为BC延长线上的一点,且FE平分∠AFD交AB于点E,试判断EF与AD之间的位置关系,并证明.