题目内容
9.已知实数$\frac{2+\sqrt{2}}{2-\sqrt{2}}$的整数部分为a,小数部分为1-b.则$\frac{(b-1)(5-b)}{\sqrt{{a}^{2}-{3}^{2}}}$的值为-1.分析 已知实数分母有理化变形后确定出a与b,代入原式计算即可求出值.
解答 解:$\frac{2+\sqrt{2}}{2-\sqrt{2}}$=$\frac{6+4\sqrt{2}}{2}$=3+2$\sqrt{2}$,
∵1<2<4,
∴1<$\sqrt{2}$<2,即5<3+2$\sqrt{2}$<6,
∴a=5,1-b=3+2$\sqrt{2}$-5,即b=3-2$\sqrt{2}$,
则原式=$\frac{(2-2\sqrt{2})(2+2\sqrt{2})}{4}$=-1.
故答案为:-1
点评 此题考查了估算无理数的大小,估算出$\sqrt{2}$的大小是解本题的关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
19.小颖把积蓄的a元零花钱存入银行,存了3年,年利率是b,到期后小颖可以取出的本息和为( )
| A. | a+3ab | B. | a(1+b)3 | C. | a+3(1+b) | D. | 3ab |
20.下列图象不能表示y是x的函数图象的是( )
| A. |  | B. |  | C. |  | D. |  |
4.在摸球实验中,暗盒内装有8个白色乒乓球和若干个黄色乒乓球,某同学进行如下试验:每次任意摸出1个球,记下颜色后放回并搅匀,再任意摸出1个球,如此重复多次试验后,得到摸出白球的频率是0.25,根据上述数据可估计盒子中黄球的个数为( )
| A. | 16个 | B. | 24个 | C. | 32个 | D. | 40个 |
14. 如图,点C、D在以AB为直径的⊙O上,且CD平分∠ACB,若AB=2,∠CBA=15°,则CD的长为( )
如图,点C、D在以AB为直径的⊙O上,且CD平分∠ACB,若AB=2,∠CBA=15°,则CD的长为( )
 如图,点C、D在以AB为直径的⊙O上,且CD平分∠ACB,若AB=2,∠CBA=15°,则CD的长为( )
如图,点C、D在以AB为直径的⊙O上,且CD平分∠ACB,若AB=2,∠CBA=15°,则CD的长为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{2}$ |
1.算式3m+n÷( )=3m-2括号中的代数式是( )
| A. | 3m+n+2 | B. | 3n-2 | C. | 3m+n+3 | D. | 3n+2 |
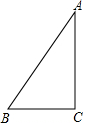 如图,在Rt△ABC中,∠C=90°,∠B=60°,将△ABC绕点A逆时针旋转60°,点B、C分别落在点B′、C′处,联结BC′与AC边交于点D,那么$\frac{BD}{DC′}$=$\frac{2}{3}$.
如图,在Rt△ABC中,∠C=90°,∠B=60°,将△ABC绕点A逆时针旋转60°,点B、C分别落在点B′、C′处,联结BC′与AC边交于点D,那么$\frac{BD}{DC′}$=$\frac{2}{3}$. 如图,D,E分别是△ABC边AB,BC上的点,AD=2BD,BE=CE,AE与CD相交于点F,若S△ABC=6,求四边形BEFD的面积.
如图,D,E分别是△ABC边AB,BC上的点,AD=2BD,BE=CE,AE与CD相交于点F,若S△ABC=6,求四边形BEFD的面积.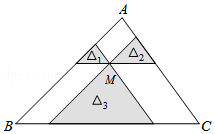 如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是1、4、25.则△ABC的面积是64.
如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是1、4、25.则△ABC的面积是64.