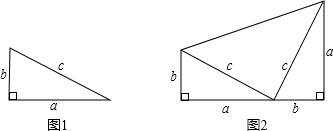
题目内容
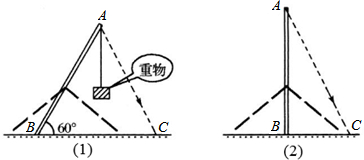
如图(1),是一起吊重物的简单装置,AB是吊杆,当它倾斜时,将重物挂起,当它逐渐直立时,重物便能逐渐升高.在阳光下,当∠ABC=60°时,量得吊杆AB的影子长BC=11.5米,很快将吊杆直立(直立过程所需时间忽略不计),如图(2),AB与地面垂直时,量得吊杆AB的影子长BC=4米,求吊杆AB的长(结果精确到1米).

考点:相似三角形的应用
专题:
分析:根据题意首先过A作AD⊥BC于点D,设AB=x,进而求出BD,AD的长,再利用相似三角形的判定与性质得出答案.
解答: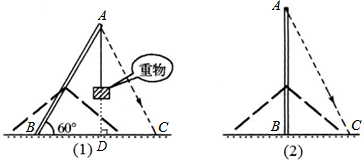 解:如图(1),过A作AD⊥BC于点D,设AB=x,
解:如图(1),过A作AD⊥BC于点D,设AB=x,
∵∠ABC=60°,
∴∠BAD=30°,
∴BD=
,则AD=
x,
∵同一时刻,太阳与地面夹角相等,
∴两图中∠ACD=∠ACB,
则△ACD∽△ACB,
故
=
,
则
=
,
解得:x1=0(不合题意舍去),x2=23-4
≈16.
答:吊杆AB的长约为16m.
 解:如图(1),过A作AD⊥BC于点D,设AB=x,
解:如图(1),过A作AD⊥BC于点D,设AB=x,∵∠ABC=60°,
∴∠BAD=30°,
∴BD=
| x |
| 2 |
| ||
| 2 |
∵同一时刻,太阳与地面夹角相等,
∴两图中∠ACD=∠ACB,
则△ACD∽△ACB,
故
| AD |
| AB |
| CD |
| BC |
则
| ||||
| x |
11.5-
| ||
| 4 |
解得:x1=0(不合题意舍去),x2=23-4
| 3 |
答:吊杆AB的长约为16m.
点评:此题主要考查了相似三角形的判定与性质以及勾股定理等知识,得出△ACD∽△ACB是解题关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 如图,△ABD≌△ACE,点B和点C是对应顶点,AB=8,AD=6,BD=7,则BE的长是( )
如图,△ABD≌△ACE,点B和点C是对应顶点,AB=8,AD=6,BD=7,则BE的长是( )| A、1 | B、2 | C、4 | D、6 |
 如图,直线y=
如图,直线y=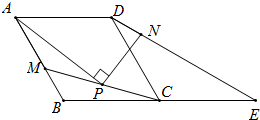 已知如图,四边形ABCD是菱形,∠ABC=120°,△DCE是等腰三角形,CD=CE,点B、C、E在一条直线上,点M是AB上的一点,P是线段MC的中点,PA⊥PN,点N在DE上.
已知如图,四边形ABCD是菱形,∠ABC=120°,△DCE是等腰三角形,CD=CE,点B、C、E在一条直线上,点M是AB上的一点,P是线段MC的中点,PA⊥PN,点N在DE上. 把一张长方形纸片(ABCD)沿GH折叠,使点B与点D重合,BD=10cm,∠DGH=55°,求∠DHC的角度.
把一张长方形纸片(ABCD)沿GH折叠,使点B与点D重合,BD=10cm,∠DGH=55°,求∠DHC的角度.