题目内容
18.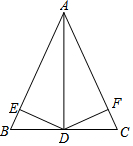 如图,AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,BE=CF.则图中全等的三角形对数是( )
如图,AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,BE=CF.则图中全等的三角形对数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由AD是△ABC的角平分线,DE⊥AB,DF⊥AC,根据角平分线的性质,可得DE=DF,∠BED=∠CFD=90°,继而证得Rt△BED≌Rt△CFD,则可得∠B=∠C,证得AB=AC,于是得到Rt△ABD≌Rt△ACD,Rt△ADE≌Rt△ADF.
解答 证明:∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,∠BED=∠CFD=90°,
在Rt△BED和Rt△CFD中,
$\left\{\begin{array}{l}{DE=DF}\\{∠BED=∠CFD}\\{BE=CF}\end{array}\right.$,
∴Rt△BED≌Rt△CFD(SAS),
∴∠B=∠C,
∴AB=AC,
∴BD=CD,
在Rt△ABD与Rt△ACD中$\left\{\begin{array}{l}{AB=AC}\\{BD=CD}\\{AD=AD}\end{array}\right.$,
∴Rt△ABD≌Rt△ACD,
在Rt△ADE与Rt△ADF中$\left\{\begin{array}{l}{DE=DF}\\{AD=AD}\end{array}\right.$,
∴Rt△ADE≌Rt△ADF.
故选C.
点评 此题考查了等腰三角形的性质与判定以及全等三角形的判定与性质.注意掌握三线合一性质的应用.

练习册系列答案
相关题目
6.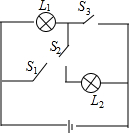 如图所示电路,任意闭合两个开关,能使灯L2亮起来的概率是( )
如图所示电路,任意闭合两个开关,能使灯L2亮起来的概率是( )
 如图所示电路,任意闭合两个开关,能使灯L2亮起来的概率是( )
如图所示电路,任意闭合两个开关,能使灯L2亮起来的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{5}$ |
10.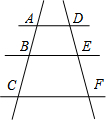 如图,AD∥BE∥CF,点B,E分别在AC,DF上,DE=2,EF=AB=3,则BC长为( )
如图,AD∥BE∥CF,点B,E分别在AC,DF上,DE=2,EF=AB=3,则BC长为( )
 如图,AD∥BE∥CF,点B,E分别在AC,DF上,DE=2,EF=AB=3,则BC长为( )
如图,AD∥BE∥CF,点B,E分别在AC,DF上,DE=2,EF=AB=3,则BC长为( )| A. | $\frac{9}{2}$ | B. | 2 | C. | $\frac{7}{2}$ | D. | 4 |
7.在Rt△ABC中,已知∠C=90°,AC=3,AB=4,则tanA的值为( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{{\sqrt{7}}}{3}$ | D. | $\frac{{\sqrt{7}}}{4}$ |
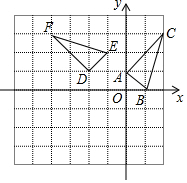 如图,△DEF是由△ABC绕着某点旋转得到的,则这点的坐标是(-1,0).
如图,△DEF是由△ABC绕着某点旋转得到的,则这点的坐标是(-1,0).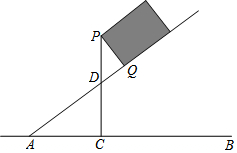 一长方形木箱沿斜面下滑,当木箱滑至如图所示位置时,AQ=m,己知木箱高PQ=h,斜面坡角α满足tanα=$\frac{3}{4}$(α为锐角),求木箱顶端P离地面AB的距离PC.
一长方形木箱沿斜面下滑,当木箱滑至如图所示位置时,AQ=m,己知木箱高PQ=h,斜面坡角α满足tanα=$\frac{3}{4}$(α为锐角),求木箱顶端P离地面AB的距离PC.