题目内容
已知二次函数图象的对称轴为x=1,且过点A(3,0)与B(0,
),则下列说法中正确的是( )
①当0≤x≤2
+1时,函数有最大值2;
②当0≤x≤2
+1时,函数有最小值-2;
③点P是第一象限内抛物线上的一个动点,则△PAB面积的最大值为
;
④对于非零实数m,当x>1+
时,y都随着x的增大而减小.
| 3 |
| 2 |
①当0≤x≤2
| 2 |
②当0≤x≤2
| 2 |
③点P是第一象限内抛物线上的一个动点,则△PAB面积的最大值为
| 3 |
| 2 |
④对于非零实数m,当x>1+
| 1 |
| m |
| A、④ | B、①② | C、③④ | D、①②③ |
考点:二次函数的性质
专题:
分析:设二次函数解析式为y=a(x-1)2+b,然后将点A、B的坐标代入求出a、b,从而得到抛物线解析式,再根据二次函数的增减性误差最大值和最小值,判断出①②正确,利用待定系数法求函数解析式求出直线AB的解析式,设过点P与y轴平行的直线与直线AB相交于点Q,表示出PQ,再利用三角形的面积公式列式整理,然后根据二次函数的最值问题求解;再根据二次函数的增减性分m是正数和负数两种情况讨论求解.
解答: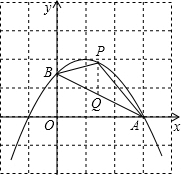 解:∵二次函数图象的对称轴为x=1,设二次函数的解析式为y=a(x-1)2+b,
解:∵二次函数图象的对称轴为x=1,设二次函数的解析式为y=a(x-1)2+b,
∴把点A(3,0)与B(0,
),代入y=a(x-1)2+b,得
,
解得
,
∴二次函数的解析式为y=-
(x-1)2+2,
∵0≤x≤2
+1,
∴当x=1时,函数有最大值2;故①正确,
当x=2
+1时,函数有最小值,最小值=-
(2
+1-1)2+2=-2,故②正确;
如图,易求直线AB的解析式为y=-
x+
,
设过点P与y轴平行的直线与直线AB相交于点Q,
则PQ=y=-
(x-1)2+2-(-
x+
)=-
x2+
x,
所以,△PAB面积=
×(-
x2+
x)×3=-
(x-
)2+
,
所以,当x=
时,△PAB的面积有最大值
,故③错误;
m<0时,1+
<1,y随x的增大而减小,
m>0时,1+
>1,y随x的增大而减大,故④错误,
综上所述,说法正确的是①②.
故选B.
 解:∵二次函数图象的对称轴为x=1,设二次函数的解析式为y=a(x-1)2+b,
解:∵二次函数图象的对称轴为x=1,设二次函数的解析式为y=a(x-1)2+b,∴把点A(3,0)与B(0,
| 3 |
| 2 |
|
解得
|
∴二次函数的解析式为y=-
| 1 |
| 2 |
∵0≤x≤2
| 2 |
∴当x=1时,函数有最大值2;故①正确,
当x=2
| 2 |
| 1 |
| 2 |
| 2 |
如图,易求直线AB的解析式为y=-
| 1 |
| 2 |
| 3 |
| 2 |
设过点P与y轴平行的直线与直线AB相交于点Q,
则PQ=y=-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
所以,△PAB面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 27 |
| 16 |
所以,当x=
| 3 |
| 2 |
| 27 |
| 16 |
m<0时,1+
| 1 |
| m |
m>0时,1+
| 1 |
| m |
综上所述,说法正确的是①②.
故选B.
点评:本题考查了二次函数的性质,主要利用了待定系数法求二次函数解析式,待定系数法求一次函数解析式,二次函数的最值问题,难点在于③表示出△PAB的面积.

练习册系列答案
相关题目
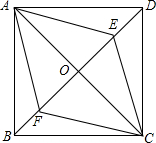 如图,在正方形ABCD中,对角线AC与BD相交于点O,点E、F在对角线BD上,且BF=DE.
如图,在正方形ABCD中,对角线AC与BD相交于点O,点E、F在对角线BD上,且BF=DE.(1)四边形AECF是什么样的特殊四边形?请说明理由;
(2)若AB=2,BF=
| ||
| 2 |
下列计算正确的是( )
| A、-1-1=0 | ||
B、-3÷
| ||
| C、(-3)2=9 | ||
| D、(-2)3=-6 |
若关于x的方程3x+(2k-1)=x-6(3k+2)的解是x=1,则k的值是( )
A、-
| ||
B、
| ||
C、
| ||
D、-
|
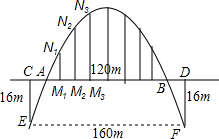 如图,要建造一座抛物线型拱桥,其水面跨度为160m,桥面主跨度AB为120m,桥面离水面高度为16m.
如图,要建造一座抛物线型拱桥,其水面跨度为160m,桥面主跨度AB为120m,桥面离水面高度为16m.