题目内容
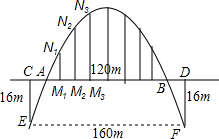如图，要建造一座抛物线型拱桥，其水面跨度为160m，桥面主跨度AB为120m，桥面离水面高度为16m．（1）求该抛物线型拱桥桥拱离桥面的最高高度；
（2）如果要在桥面上每隔15m设置一根钢索，垂直于桥面连接到桥拱上，请问，共需要钢索多少米？（不计穿过桥拱和桥面部分钢索长度，精确到1m）．
考点：二次函数的应用
专题：
分析：（1）以桥面所在的直线CD为x轴，以过桥拱的顶点的直线为y轴，建立平面直角坐标系，就可以求出A、B、E、F的坐标，设抛物线的解析式为y=ax2+c，由待定系数法求出其解即可；
（2）先由各根钢索在桥面上的连接点分别为-45，-30，-15，0，15，30，45，由抛物线的对称性只要求出横坐标为0，15，30，45就可以求出结论．
（2）先由各根钢索在桥面上的连接点分别为-45，-30，-15，0，15，30，45，由抛物线的对称性只要求出横坐标为0，15，30，45就可以求出结论．
解答：解：（1）以桥面所在的直线CD为x轴，以过桥拱的顶点的直线为y轴，建立平面直角坐标系，
∴A（-60，0），B（60，0）．E（-80，-16）
设抛物线的解析式为y=ax2+c，由题意，得
，
解得：
，
∴y=-
x2+
，
∴当x=0时，y=
．
答：该抛物线型拱桥桥拱离桥面的最高高度为
；
（2）由题意，得
当x=0时，y=
，
当x=15时，y=
，
当x=30时，y=
，
当x=45时，y=9．
故钢索的总长度为：
+2×
+2×
+2×9=108米．
答：共需要钢索108米．
∴A（-60，0），B（60，0）．E（-80，-16）
设抛物线的解析式为y=ax2+c，由题意，得
|
解得：
|
∴y=-
| 1 |
| 175 |
| 144 |
| 7 |
∴当x=0时，y=
| 144 |
| 7 |
答：该抛物线型拱桥桥拱离桥面的最高高度为
| 144 |
| 7 |
（2）由题意，得
当x=0时，y=
| 144 |
| 7 |
当x=15时，y=
| 135 |
| 7 |
当x=30时，y=
| 108 |
| 7 |
当x=45时，y=9．
故钢索的总长度为：
| 144 |
| 7 |
| 135 |
| 7 |
| 108 |
| 7 |
答：共需要钢索108米．
点评：本题考查了运用待定系数法求二次函数的解析式的运用，由自变量的值求函数值的运用，解答时求出函数的解析式是关键．
练习册系列答案
相关题目
如图，BD是⊙O的直径，点A在BD的延长线上，AC切⊙O于点C，∠A=30°，则∠B=（ ）| A、60° | B、30° |
| C、15° | D、45° |
6tan45°的值等于（ ）
A、6
| ||
B、3
| ||
| C、6 | ||
D、2
|