题目内容
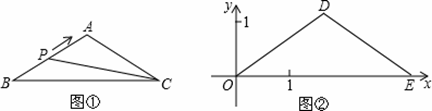
如图①,在△ABC中,AB=AC,BC=acm,∠B=30°.动点P以1cm/s的速度从点B出发,沿折线B-A-C运动到点C时停止运动.设点P出发x s时,△PBC的面积为y cm2.已知y与x的函数图象如图②所示.请根据图中信息,解答下列问题:
(1)试判断△DOE的形状,并说明理由;
(2)当a为何值时,△DOE与△ABC相似?
解:
(1)△DOE是等腰三角形.
作DF⊥OE于F,
∵AB=AC,点P以1cm/s的速度运动,
∴点P在边AB和AC上的运动时间相同,
∴点F是OE的中点,
∴DF是OE的垂直平分线,
∴DO=DE,
∴△DOE是等腰三角形.
| |

练习册系列答案
相关题目
 ,0),B(
,0),B(
 ”,小明做了下列三个模拟实验来验证。
”,小明做了下列三个模拟实验来验证。
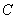 变化,使60º
变化,使60º  90º时,求出a的取值范围;
90º时,求出a的取值范围; 交
交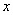 轴于点
轴于点 ,问:在
,问:在 轴上是否存在点
轴上是否存在点 ,使得△
,使得△ 是一个等腰直角三角形?若存在,请求出
是一个等腰直角三角形?若存在,请求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.