题目内容
已知抛物线y=ax2+bx+c(a>0)与x轴的两个交点分别为A
(-1,0)、B(3,0),与y轴的交点为点D,顶点为C,
(1)写出该抛物线的对称轴方程;
(2)当点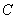 变化,使60º
变化,使60º  90º时,求出a的取值范围;
90º时,求出a的取值范围;
(3)作直线 交
交 轴于点
轴于点 ,问:在
,问:在 轴上是否存在点
轴上是否存在点 ,使得△
,使得△ 是一个等腰直角三角形?若存在,请求出
是一个等腰直角三角形?若存在,请求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.

| |
(1) 直线x=1;
(2) 当 时,
时, 为等边三角形,
为等边三角形,
设 ,C点代入得
,C点代入得 
当 时,
时, 为等腰直角三角形,即
为等腰直角三角形,即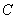 (1,-2)
(1,-2)
同理可得 
 所以
所以
(3)由于 ,
,
 ,故
,故
分三种情况讨论:
如图1可证明 得
得



‚ 如图2可证明 得
得



③如图3可证明 得
得


综上,  、
、  和
和

练习册系列答案
相关题目
 、
、 为
为 米,主塔
米,主塔 的仰角为
的仰角为
 °,且
°,且 的长度为
的长度为 米,求该桥的主塔
米,求该桥的主塔

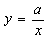
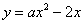
 的解为
的解为 ,则函数
,则函数 图象与
图象与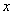 轴的交点是( )
轴的交点是( ) B.
B. C.
C. D.
D.