题目内容
10.已知关于x的方程x2-2(k-3)x+k2-4k-1=0有实数根.(1)求k的取值范围;
(2)当k取满足条件的最大整数时,求方程的解.
分析 (1)根据关于x的方程x2-2(k-3)x+k2-4k-1=0有实数根.则△≥0,列出不等式,即可求出k的取值范围.
(2)由(1)中k的取值范围得出符合条件的k的最大整数值,代入原方程,利用求根公式即可求出x的值.
解答 解:(1)△=[-2(k-3)]2-4(k2-4k-1)=-8k+40,
∵关于x的方程x2-2(k-3)x+k2-4k-1=0有实数根.
∴-8k+40≥0,解得k≤5.
(2)当k为符合条件的最大整数时,k=5.
此时方程化为x2-4x+4=0,
此时方程的根为x1=x2=2.
点评 本题考查的是一元二次方程ax2+bx+c=0(a≠0)的根与△的关系及求根公式,是一个综合性的题目,难度适中.

练习册系列答案
相关题目
 如图,在矩形ABCD中,AB=6cm,BC=8cm,点P从A开始沿AB边向点B以1cm/s的速度移动,点Q从点B边开始沿BC边向点C以2cm/s的速度移动.
如图,在矩形ABCD中,AB=6cm,BC=8cm,点P从A开始沿AB边向点B以1cm/s的速度移动,点Q从点B边开始沿BC边向点C以2cm/s的速度移动.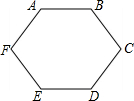 从图中的某个顶点出发,与其余各顶点相连结,可以把这个图形分割成4个三角形.(先想一想,然后动手画一画、数一数)
从图中的某个顶点出发,与其余各顶点相连结,可以把这个图形分割成4个三角形.(先想一想,然后动手画一画、数一数)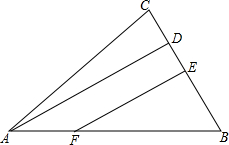 已知:如图,AD⊥BC于D,E为BC中点,EF⊥BC交AB于F,AB=9cm,BC=6cm,DC=2cm,求AF的长.
已知:如图,AD⊥BC于D,E为BC中点,EF⊥BC交AB于F,AB=9cm,BC=6cm,DC=2cm,求AF的长.