题目内容
 如图,已知一次函数y1=-x+m与二次函数y2=ax2+bx-3的图象相交于点A(-1,0)、B(2,-3),且二次函数与y轴相交于点C.
如图,已知一次函数y1=-x+m与二次函数y2=ax2+bx-3的图象相交于点A(-1,0)、B(2,-3),且二次函数与y轴相交于点C.(1)求点m的值和二次函数的表达式;
(2)求出抛物线的顶点P的坐标及△ABP的面积;
(3)请直接写出当y1>y2时,自变量的取值范围.
考点:二次函数的性质,二次函数与不等式(组)
专题:
分析:(1)把点A的坐标代入一次函数计算即可求出m,再把点A、B的坐标代入二次函数解析式,利用待定系数法求解即可;
(2)把二次函数解析式整理成顶点式形式,然后写出顶点P的坐标,再求出对称轴与直线AB的交点坐标,然后利用三角形的面积公式列式计算即可得解;
(3)根据函数图象写出一次函数图象在二次函数图象上方部分的x的取值范围即可.
(2)把二次函数解析式整理成顶点式形式,然后写出顶点P的坐标,再求出对称轴与直线AB的交点坐标,然后利用三角形的面积公式列式计算即可得解;
(3)根据函数图象写出一次函数图象在二次函数图象上方部分的x的取值范围即可.
解答: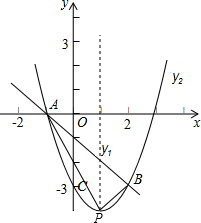 解:(1)点A(-1,0)代入y1=-x+m得,1+m=0,
解:(1)点A(-1,0)代入y1=-x+m得,1+m=0,
解得m=-1,
∵二次函数y2=ax2+bx-3经过A(-1,0)、B(2,-3),
∴
,
解得
,
所以,二次函数的解析式为y2=x2-2x-3;
(2)∵y2=x2-2x-3=(x-1)2-4,
∴顶点坐标为(1,-4),
当x=1时,y1=-1-1=-2,
∴△ABP的面积=
×[-2-(-4)]×(1+3)=4;
(3)y1>y2时,-1<x<3.
 解:(1)点A(-1,0)代入y1=-x+m得,1+m=0,
解:(1)点A(-1,0)代入y1=-x+m得,1+m=0,解得m=-1,
∵二次函数y2=ax2+bx-3经过A(-1,0)、B(2,-3),
∴
|
解得
|
所以,二次函数的解析式为y2=x2-2x-3;
(2)∵y2=x2-2x-3=(x-1)2-4,
∴顶点坐标为(1,-4),
当x=1时,y1=-1-1=-2,
∴△ABP的面积=
| 1 |
| 2 |
(3)y1>y2时,-1<x<3.
点评:本题考查了二次函数的性质,二次函数与不等式,主要利用了待定系数法求一次函数解析式,待定系数法求二次函数解析式,以及二次函数与不等式的关系,熟记性质并利用数形结合的思想求解是解题的关键.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
-(-5)的绝对值是( )
| A、5 | ||
| B、-5 | ||
C、
| ||
D、-
|
下列各组长度的线段能构成三角形的是( )
| A、1.5cm,3.9cm,2.3cm |
| B、3.5cm,7.1cm,3.6cm |
| C、6cm,1cm,6cm |
| D、4cm,10cm,4cm |
计算(-4)2的值是( )
| A、16 | B、-16 | C、8 | D、-8 |
下列合并同类项正确的是( )
| A、2x2+3x4=5x6 |
| B、5xy2-3xy2=2 |
| C、7m2n-7mn2 |
| D、4ab2-5ab2=-ab2 |
 如图,在长和宽分别是a、b的长方纸片的四个角都剪去一个边长为x的正方形,当a=8,b=6,且剪去部分的面积等于剩余部分的面积的
如图,在长和宽分别是a、b的长方纸片的四个角都剪去一个边长为x的正方形,当a=8,b=6,且剪去部分的面积等于剩余部分的面积的 如图所示,将长方形纸片ABCD沿直线EF折叠,点C、D分别落在点C′、D′上,已知∠EFC=66°,求∠AED′的度数.
如图所示,将长方形纸片ABCD沿直线EF折叠,点C、D分别落在点C′、D′上,已知∠EFC=66°,求∠AED′的度数.