题目内容
8.如图1~4,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为S1,S2,S3,…,S10,则S1+S2+S3+…+S10=π.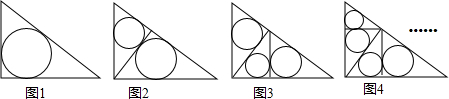
分析 (1)图1,作辅助线构建正方形OECF,设圆O的半径为r,根据切线长定理表示出AD和BD的长,利用AD+BD=5列方程求出半径r=$\frac{a+b-c}{2}$(a、b是直角边,c为斜边),运用圆面积公式=πr2求出面积=π;
(2)图2,先求斜边上的高CD的长,再由勾股定理求出AD和BD,利用半径r=$\frac{a+b-c}{2}$(a、b是直角边,c为斜边)求两个圆的半径,从而求出两圆的面积和=π;
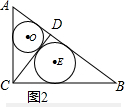
(3)图3,继续求高DM和CM、BM,利用半径r=$\frac{a+b-c}{2}$(a、b是直角边,c为斜边)求三个圆的半径,从而求出三个圆的面积和=π;
综上所述:发现S1+S2+S3+…+S10=π.
解答 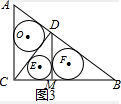
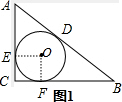 解:(1)图1,过点O做OE⊥AC,OF⊥BC,垂足为E、F,则∠OEC=∠OFC=90°
解:(1)图1,过点O做OE⊥AC,OF⊥BC,垂足为E、F,则∠OEC=∠OFC=90°
∵∠C=90°
∴四边形OECF为矩形
∵OE=OF
∴矩形OECF为正方形
设圆O的半径为r,则OE=OF=r,AD=AE=3-r,BD=4-r
∴3-r+4-r=5,r=$\frac{3+4-5}{2}$=1
∴S1=π×12=π
(2)图2,由S△ABC=$\frac{1}{2}$×3×4=$\frac{1}{2}$×5×CD
∴CD=$\frac{12}{5}$
由勾股定理得:AD=$\sqrt{{3}^{2}-(\frac{12}{5})^{2}}$=$\frac{9}{5}$,BD=5-$\frac{9}{5}$=$\frac{16}{5}$
由(1)得:⊙O的半径=$\frac{\frac{9}{5}+\frac{12}{5}-3}{2}$=$\frac{3}{5}$,⊙E的半径=$\frac{\frac{12}{5}+\frac{16}{5}-4}{2}$=$\frac{4}{5}$
∴S1+S2=π×$(\frac{3}{5})^{2}$+π×$(\frac{4}{5})^{2}$=π
(3)图3,由S△CDB=$\frac{1}{2}$×$\frac{12}{5}$×$\frac{16}{5}$=$\frac{1}{2}$×4×MD
∴MD=$\frac{48}{25}$
由勾股定理得:CM=$\sqrt{(\frac{12}{5})^{2}-(\frac{48}{25})^{2}}$=$\frac{36}{25}$,MB=4-$\frac{36}{25}$=$\frac{64}{25}$
由(1)得:⊙O的半径=$\frac{3}{5}$,:⊙E的半径=$\frac{\frac{48}{25}+\frac{36}{25}-\frac{12}{5}}{2}$=$\frac{12}{25}$,:⊙F的半径=$\frac{\frac{48}{25}+\frac{64}{25}-\frac{16}{5}}{2}$=$\frac{16}{25}$
∴S1+S2+S3=π×$(\frac{3}{5})^{2}$+π×$(\frac{12}{25})^{2}$+π×$(\frac{16}{25})^{2}$=π
∴图4中的S1+S2+S3+S4=π
则S1+S2+S3+…+S10=π
故答案为:π.
点评 本题考查了直角三角形的内切圆,这是一个图形变化类的规律题,首先应找出图形哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解;解决此题的思路为:①先找出计算直角三角形内切圆半径的规律:半径r=$\frac{a+b-c}{2}$(a、b是直角边,c为斜边);②利用面积相等计算斜边上的高;③运用勾股定理计算直角三角形的边长.

 阅读快车系列答案
阅读快车系列答案| A. | 0.36×107 | B. | 3.6×106 | C. | 3.6×107 | D. | 36×105 |
 如图,A,B,C是⊙O上三个点,∠ACB=30°,则∠BAO的度数是( )
如图,A,B,C是⊙O上三个点,∠ACB=30°,则∠BAO的度数是( )| A. | 55° | B. | 60° | C. | 65° | D. | 70° |
| A. | y=-$\sqrt{3}x+3$ | B. | y=-$\frac{\sqrt{3}}{3}x+1$ | C. | y=$\sqrt{3}x+1$ | D. | y=$\frac{\sqrt{3}}{3}x+1$ |

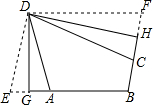 定义:有三个内角相等的四边形叫三等角四边形.
定义:有三个内角相等的四边形叫三等角四边形. 如图,把一块三角板的60°角的顶点放在直尺的一边上,若∠1=2∠2,则∠1=80°.
如图,把一块三角板的60°角的顶点放在直尺的一边上,若∠1=2∠2,则∠1=80°. 如图,点A、C、D、B四点共线,且AC=BD,∠A=∠B,∠ADE=∠BCF,求证:DE=CF.
如图,点A、C、D、B四点共线,且AC=BD,∠A=∠B,∠ADE=∠BCF,求证:DE=CF.