题目内容
11.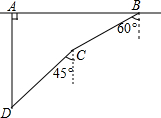 如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).
如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).
分析 过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F,则∠E=∠F=90°,拦截点D处到公路的距离DA=BE+CF.解Rt△BCE,求出BE=$\frac{1}{2}$BC=$\frac{1}{2}$×1000=500米;解Rt△CDF,求出CF=$\frac{\sqrt{2}}{2}$CD=500$\sqrt{2}$米,则DA=BE+CF=(500+500$\sqrt{2}$)米.
解答 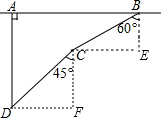 解:如图,过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F,则∠E=∠F=90°,拦截点D处到公路的距离DA=BE+CF.
解:如图,过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F,则∠E=∠F=90°,拦截点D处到公路的距离DA=BE+CF.
在Rt△BCE中,∵∠E=90°,∠CBE=60°,
∴∠BCE=30°,
∴BE=$\frac{1}{2}$BC=$\frac{1}{2}$×1000=500米;
在Rt△CDF中,∵∠F=90°,∠DCF=45°,CD=BC=1000米,
∴CF=$\frac{\sqrt{2}}{2}$CD=500$\sqrt{2}$米,
∴DA=BE+CF=(500+500$\sqrt{2}$)米,
故拦截点D处到公路的距离是(500+500$\sqrt{2}$)米.
点评 本题考查了解直角三角形的应用-方向角问题,锐角三角函数的定义,正确理解方向角的定义,进而作出辅助线构造直角三角形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.不等式2x-1>0的解集是( )
| A. | x>$\frac{1}{2}$ | B. | x<$\frac{1}{2}$ | C. | x>-$\frac{1}{2}$ | D. | x<-$\frac{1}{2}$ |
 阅读材料:
阅读材料: 如图,四边形ABCD中,∠A=90°,AB=3$\sqrt{3}$,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为3.
如图,四边形ABCD中,∠A=90°,AB=3$\sqrt{3}$,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为3.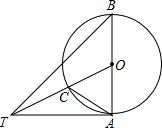 如图,AB是⊙O的直径,∠ABT=45°,AT=AB.
如图,AB是⊙O的直径,∠ABT=45°,AT=AB. 如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E.若∠CBF=20°,则∠AED等于65度.
如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E.若∠CBF=20°,则∠AED等于65度.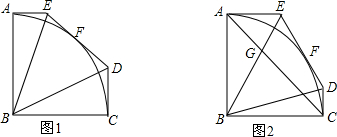
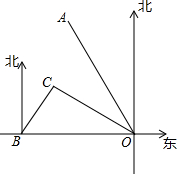 如图所示,港口B位于港口O正西方向120km处,小岛C位于港口O北偏西60°的方向.一艘游船从港口O出发,沿OA方向(北偏西30°)以vkm/h的速度驶离港口O,同时一艘快艇从港口B出发,沿北偏东30°的方向以60km/h的速度驶向小岛C,在小岛C用1h加装补给物资后,立即按原来的速度给游船送去.
如图所示,港口B位于港口O正西方向120km处,小岛C位于港口O北偏西60°的方向.一艘游船从港口O出发,沿OA方向(北偏西30°)以vkm/h的速度驶离港口O,同时一艘快艇从港口B出发,沿北偏东30°的方向以60km/h的速度驶向小岛C,在小岛C用1h加装补给物资后,立即按原来的速度给游船送去.