题目内容
20.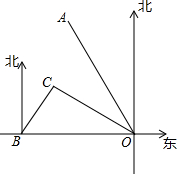 如图所示,港口B位于港口O正西方向120km处,小岛C位于港口O北偏西60°的方向.一艘游船从港口O出发,沿OA方向(北偏西30°)以vkm/h的速度驶离港口O,同时一艘快艇从港口B出发,沿北偏东30°的方向以60km/h的速度驶向小岛C,在小岛C用1h加装补给物资后,立即按原来的速度给游船送去.
如图所示,港口B位于港口O正西方向120km处,小岛C位于港口O北偏西60°的方向.一艘游船从港口O出发,沿OA方向(北偏西30°)以vkm/h的速度驶离港口O,同时一艘快艇从港口B出发,沿北偏东30°的方向以60km/h的速度驶向小岛C,在小岛C用1h加装补给物资后,立即按原来的速度给游船送去.(1)快艇从港口B到小岛C需要多长时间?
(2)若快艇从小岛C到与游船相遇恰好用时1h,求v的值及相遇处与港口O的距离.
分析 (1)要求B到C的时间,已知其速度,则只要求得BC的路程,再利用路程公式即可求得所需的时间;
(2)过C作CD⊥OA,垂足为D,设相会处为点E.求出OC=OB•cos30°=60$\sqrt{3}$,CD=$\frac{1}{2}$OC=30$\sqrt{3}$,OD=OC•cos30°=90,则DE=90-3v.在直角△CDE中利用勾股定理得出CD2+DE2=CE2,即(30$\sqrt{3}$)2+(90-3v)2=602,解方程求出v=20或40,进而求出相遇处与港口O的距离.
解答 解:(1)∵∠CBO=60°,∠COB=30°,
∴∠BCO=90°.
在Rt△BCO中,∵OB=120,
∴BC=$\frac{1}{2}$OB=60,
∴快艇从港口B到小岛C的时间为:60÷60=1(小时); (2)过C作CD⊥OA,垂足为D,设相会处为点E.
(2)过C作CD⊥OA,垂足为D,设相会处为点E.
则OC=OB•cos30°=60$\sqrt{3}$,CD=$\frac{1}{2}$OC=30$\sqrt{3}$,OD=OC•cos30°=90,
∴DE=90-3v.
∵CE=60,CD2+DE2=CE2,
∴(30$\sqrt{3}$)2+(90-3v)2=602,
∴v=20或40,
∴当v=20km/h时,OE=3×20=60km,
当v=40km/h时,OE=3×40=120km.
点评 此题考查了解直角三角形的应用-方向角问题,锐角三角函数的定义,勾股定理等知识,理解方向角的定义,得出∠BCO=90°是解题的关键,本题难易程度适中.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
10. 一个几何体的三视图如图所示,则这个几何体是( )
一个几何体的三视图如图所示,则这个几何体是( )
 一个几何体的三视图如图所示,则这个几何体是( )
一个几何体的三视图如图所示,则这个几何体是( )| A. | 三棱锥 | B. | 三棱柱 | C. | 圆柱 | D. | 长方体 |
8.下列图案中,轴对称图形是( )
| A. |  | B. |  | C. |  | D. |  |
15. 如图所示的几何体为圆台,其俯视图正确的是( )
如图所示的几何体为圆台,其俯视图正确的是( )
 如图所示的几何体为圆台,其俯视图正确的是( )
如图所示的几何体为圆台,其俯视图正确的是( )| A. |  | B. |  | C. |  | D. |  |
5.济南某中学足球队的18名队员的年龄如表所示:
这18名队员年龄的众数和中位数分别是( )
| 年龄(单位:岁) | 12 | 13 | 14 | 15 |
| 人数 | 3 | 5 | 6 | 4 |
| A. | 13岁,14岁 | B. | 14岁,14岁 | C. | 14岁,13岁 | D. | 14岁,15岁 |
12.下列图形既是中心对称又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
9.某校篮球队13名同学的身高如下表:
则该校篮球队13名同学身高的众数和中位数分别是( )
| 身高(cm) | 175 | 180 | 182 | 185 | 188 |
| 人数(个) | 1 | 5 | 4 | 2 | 1 |
| A. | 182,180 | B. | 180,180 | C. | 180,182 | D. | 188,182 |
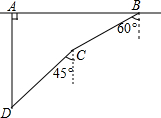 如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).
如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值). 在边长为1的小正方形网格中,△AOB的顶点均在格点上,
在边长为1的小正方形网格中,△AOB的顶点均在格点上,