题目内容
17.计算:(1)(+3)+(-5)-4-(-2);
(2)-54×$2\frac{1}{4}÷$(-4$\frac{1}{2}$)×$\frac{2}{9}$
(3)($\frac{7}{9}$-1$\frac{1}{6}$-$\frac{7}{18}$)÷(-$\frac{1}{36}$);
(4)-16-|-5|+2×(-$\frac{1}{2}$)2.
分析 (1)原式利用减法法则变形,计算即可得到结果;
(2)原式从左到右依次计算即可得到结果;
(3)原式利用除法法则变形,再利用乘法分配律计算即可得到结果;
(4)原式先计算乘方运算,再计算乘法运算,最后算加减运算即可得到结果.
解答 解:(1)原式=3-5-4+2=-4;
(2)原式=54×$\frac{9}{4}$×$\frac{2}{9}$×$\frac{2}{9}$=6;
(3)原式=($\frac{7}{9}$-1$\frac{1}{6}$-$\frac{7}{18}$)×(-36)=-28+42+14=28;
(4)原式=-1-5+2×$\frac{1}{4}$=-1-5+$\frac{1}{2}$=-5$\frac{1}{2}$.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
5. 如图,AC=AD,BC=BD,则有( )
如图,AC=AD,BC=BD,则有( )
 如图,AC=AD,BC=BD,则有( )
如图,AC=AD,BC=BD,则有( )| A. | AB与CD互相垂直平分 | B. | CD垂直平分AB | ||
| C. | AB垂直平分CD | D. | CD平分∠ACB |
12.当x=2时,代数式ax3+bx+1值为3,那么当x=-2时,代数式ax3+bx+1的值是 ( )
| A. | -3 | B. | 1 | C. | -1 | D. | 2 |
2.民谚有云:“不到庐山辜负目,不食螃蟹辜负腹.”,又到了食蟹的好季节啦!某经销商去水产批发市场采购太湖蟹,他看中了A、B两家的某种品质相近的太湖蟹.零售价都为60元/千克,批发价各不相同.
A家规定:批发数量不超过100千克,按零售价的92%优惠;批发数量超过100千克但不超过200千克,按零售价的90%优惠;超过200千克的按零售价的88%优惠.
B家的规定如下表:
(1)如果他批发90千克太湖蟹,则他在A家批发需要4968元,在B家批发需要4890元;
(2)如果他批发x千克太湖蟹(150<x<200),则他在A家批发需要54x元,在B家批发需要45x+1200元(用含x的代数式表示);
(3)现在他要批发170千克太湖蟹,你能帮助他选择在哪家批发更优惠吗?请说明理由.
A家规定:批发数量不超过100千克,按零售价的92%优惠;批发数量超过100千克但不超过200千克,按零售价的90%优惠;超过200千克的按零售价的88%优惠.
B家的规定如下表:
| 数量范围 (千克) | 0~50部分 (含50) | 50以上~150部分(含150,不含50) | 150以上~250部分(含250,不含150) | 250以上部分 (不含250) |
| 价 格(元) | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
(2)如果他批发x千克太湖蟹(150<x<200),则他在A家批发需要54x元,在B家批发需要45x+1200元(用含x的代数式表示);
(3)现在他要批发170千克太湖蟹,你能帮助他选择在哪家批发更优惠吗?请说明理由.
6.有三张正面分别写有数字-2,-1,1的卡片,它们的背面完全相同,将这三张卡片背面朝上洗匀后随机抽取一张,以其正面的数字作为点P的横坐标,然后再从剩余的两张卡片中随机抽取一张,以其正面的数字作为点P的纵坐标,则点P在第二象限的槪率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
 如图,在△ABC中,∠ACB=90°,AD平分∠BAC,EF⊥AD,分别交AB,AC,AD及BC的延长线于点E、F、H、G,求证:2∠G+∠B=90°.
如图,在△ABC中,∠ACB=90°,AD平分∠BAC,EF⊥AD,分别交AB,AC,AD及BC的延长线于点E、F、H、G,求证:2∠G+∠B=90°. 如图,是4×4正方形网格,其中已有4个小方格涂成了黑色,现在要从其余12个白色小方格中选出一个也涂成黑色,使整个黑色部分图形构成轴对称图形,这样的白色小方格有3个.
如图,是4×4正方形网格,其中已有4个小方格涂成了黑色,现在要从其余12个白色小方格中选出一个也涂成黑色,使整个黑色部分图形构成轴对称图形,这样的白色小方格有3个.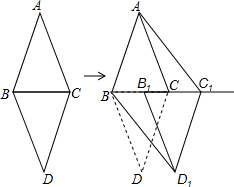 如图,△ABC和△DBC是两个具有公共边的全等三角形,AB=AC=6cm,BC=4cm,将△DBC沿射线BC平移一定的距离得到△D1B1C1,连接AC1,BD1.如果四边形ABD1C1是矩形,那么平移的距离为( )
如图,△ABC和△DBC是两个具有公共边的全等三角形,AB=AC=6cm,BC=4cm,将△DBC沿射线BC平移一定的距离得到△D1B1C1,连接AC1,BD1.如果四边形ABD1C1是矩形,那么平移的距离为( )