题目内容
6.有三张正面分别写有数字-2,-1,1的卡片,它们的背面完全相同,将这三张卡片背面朝上洗匀后随机抽取一张,以其正面的数字作为点P的横坐标,然后再从剩余的两张卡片中随机抽取一张,以其正面的数字作为点P的纵坐标,则点P在第二象限的槪率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
分析 画出树状图,然后确定出在第二象限的点的个数,再根据概率公式列式进行计算即可得解.
解答 解:根据题意,画出树状图如下: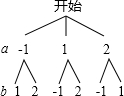
一共有6种情况,在第二象限的点有(-1,1)(-1,2)共2个,
所以,P=$\frac{2}{6}$=$\frac{1}{3}$.
故选B.
点评 本题考查了列表法与树状图法,第二象限点的坐标特征,用到的知识点为:概率=所求情况数与总情况数之比,熟记概率公式是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.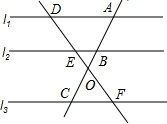 如图l1∥l2∥l3,直线AC与DF交于点O,且与l1,l2,l3分别交于点A,B,C,D,E,F,则下列比例式不正确的是( )
如图l1∥l2∥l3,直线AC与DF交于点O,且与l1,l2,l3分别交于点A,B,C,D,E,F,则下列比例式不正确的是( )
 如图l1∥l2∥l3,直线AC与DF交于点O,且与l1,l2,l3分别交于点A,B,C,D,E,F,则下列比例式不正确的是( )
如图l1∥l2∥l3,直线AC与DF交于点O,且与l1,l2,l3分别交于点A,B,C,D,E,F,则下列比例式不正确的是( )| A. | $\frac{AB}{BC}$=$\frac{DE}{EF}$ | B. | $\frac{AB}{BO}$=$\frac{DE}{EO}$ | C. | $\frac{OB}{OC}$=$\frac{OE}{OF}$ | D. | $\frac{AD}{CF}$=$\frac{AO}{AC}$ |
 如图,在△ABC中,E是内心,延长AE交△ABC的外接圆于点D.试说明:DE=DB.
如图,在△ABC中,E是内心,延长AE交△ABC的外接圆于点D.试说明:DE=DB.
 用圆规、直尺作图,不写作法,但要保留作图痕迹.
用圆规、直尺作图,不写作法,但要保留作图痕迹.