题目内容
8. 如图,把一张长方形纸片ABCD沿EF折叠,若∠EFG=50°,则∠BGE=( )
如图,把一张长方形纸片ABCD沿EF折叠,若∠EFG=50°,则∠BGE=( )| A. | 100° | B. | 90° | C. | 80° | D. | 70° |
分析 先根据平行线的性质得出∠DEF=∠EFG,再由图形翻折变换的性质得出∠GEF=∠DEF,根据三角形外角的性质即可得出结论.
解答 解:∵四边形纸片ABCD是矩形纸片,
∴AD∥BC.
∴∠DEF=∠EFG,
又∵∠EFG=50°,
∴∠DEF=50°,
∵四边形EFC′D′由四边形EFCD翻折而成,
∴∠GEF=∠DEF=50°,
∴∠EGB=50°+50°=100°.
故选A.
点评 本题考查的是平行线的性质,图形翻折变换的性质及矩形的性质,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,只是上的位置变化.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
3.已知∠A=45°,则∠A的补角等于( )
| A. | 45° | B. | 90° | C. | 135° | D. | 180° |
18.当你乘车沿一条平坦的大道向前行驶时,你会发现,前方那些高一些的建筑物好像“沉”到了位于它们前面那些矮一些的建筑物后面去了,这是因为( )
| A. | 汽车开的很快 | B. | 盲区减小 | C. | 盲区增大 | D. | 无法确定 |
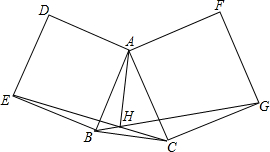 在△ABC的边AB,AC向外作正方形ABED,ACGF,BG、CE相交于H.求证:AH⊥BC.
在△ABC的边AB,AC向外作正方形ABED,ACGF,BG、CE相交于H.求证:AH⊥BC. 如图,点P是平行四边形ABCD对角线BD上的动点,点M为AD的中点,已知AD=8,AB=10,∠ABD=45°,把平行四边形ABCD绕着点A按逆时针方向旋转,点P的对应点是点Q,则线段MQ的长度的最大值与最小值的差为18-5$\sqrt{2}$.
如图,点P是平行四边形ABCD对角线BD上的动点,点M为AD的中点,已知AD=8,AB=10,∠ABD=45°,把平行四边形ABCD绕着点A按逆时针方向旋转,点P的对应点是点Q,则线段MQ的长度的最大值与最小值的差为18-5$\sqrt{2}$.