题目内容
5.解方程组:$\left\{\begin{array}{l}{{x}^{2}+4xy+4{y}^{2}=9}\\{{x}^{2}-xy=0}\end{array}\right.$.分析 由①得出x+2y=3,x+2y=-3③,由②得出x=0,x-y=0,则原方程组可化为四个二元一次方程组,求出方程组的解即可.
解答 解:$\left\{\begin{array}{l}{{x}^{2}+4xy+4{y}^{2}=9①}\\{{x}^{2}-xy=0②}\end{array}\right.$
由①得:(x+2y)2=9,
即得x+2y=3,x+2y=-3③,
由②得:x(x-y)=0,
即x=0,x-y=0,
则原方程组可化为
$\left\{\begin{array}{l}{x+2y=3}\\{x=0}\end{array}\right.$,$\left\{\begin{array}{l}{x+2y=3}\\{x-y=0}\end{array}\right.$,$\left\{\begin{array}{l}{x+2y=-3}\\{x=0}\end{array}\right.$,$\left\{\begin{array}{l}{x+2y=-3}\\{x-y=0}\end{array}\right.$,
解得,即可得出原方程组的解:$\left\{\begin{array}{l}{{x}_{1}=0}\\{{y}_{2}=6}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=1}\\{{y}_{2}=1}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{3}=0}\\{{y}_{3}=-0.5}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{4}=-1}\\{{y}_{4}=-1}\end{array}\right.$.
点评 本考查了解高次方程组,能把高次方程组转化成二元一次方程组是解此题的关键.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案| A. | 2007 | B. | 2008 | C. | 2009 | D. | 2010 |
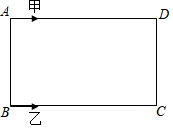 如图,甲、乙两位同学在长方形的场地ABCD上绕着四周跑步,甲沿着A-D-C-B-A方向循环跑步,同时乙沿着B-C-D-A-B方向循环跑步,AB=30米,BC=50米,若甲速度为2米/秒,乙速度3米/秒.
如图,甲、乙两位同学在长方形的场地ABCD上绕着四周跑步,甲沿着A-D-C-B-A方向循环跑步,同时乙沿着B-C-D-A-B方向循环跑步,AB=30米,BC=50米,若甲速度为2米/秒,乙速度3米/秒.