题目内容
2．解答下列问题：（1）若已知直线l上依次有点A1，A2，A3…、A25共25个点，要确定一点P，到已知各点的距离之和最小，则点P的位置应取在点A13处．
（2）若已知直线l上有点A1，A2，A3…、A50共50个点，要确定一点P，使它到已知各点的距离之和最小，则点P的位置应取在点A25和A26之间的任何地方．
分析 P的位置应取这些点正中间的点，25÷2=12，那么中间的点是第13个点；有50个点时，正中间有2个数，50÷2=25，应是第25和第26个点之间的任意部分．
解答 解：P的位置应取这些点正中间的点，25÷2=12，那么中间的点是第13个点，点A13处；
有50个点时，正中间有2个数，50÷2=25，应是第25和第26个点之间的任意部分，点A25和A26之间的任何地方．
故答案为：点A13处；点A25和A26之间的任何地方．
点评 此题考查直线，射线，线段；掌握当数轴上有奇数个点时，数轴上到到这些点的距离之和最小的点是正中间那个点；当数轴上有偶数个点时，数轴上到到这些点的距离之和最小的点是正中间两个点之间的部分是解决问题的关键．
练习册系列答案
高效智能课时作业系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
12．
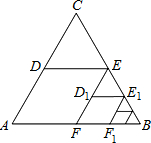如图，△ABC是边长为1的等边三角形．取BC边中点E，作ED∥AB，EF∥AC，得到四边形EDAF，它的面积记作S1；取BE中点E1，作E1D1∥FB，E1F1∥EF，得到四边形E1D1FF1，它的面积记作S2；…；照此规律作下去，则S5为（ ）
如图，△ABC是边长为1的等边三角形．取BC边中点E，作ED∥AB，EF∥AC，得到四边形EDAF，它的面积记作S1；取BE中点E1，作E1D1∥FB，E1F1∥EF，得到四边形E1D1FF1，它的面积记作S2；…；照此规律作下去，则S5为（ ）| A． | $\frac{\sqrt{3}}{8}$×（$\frac{1}{4}$）4 | B． | $\frac{\sqrt{3}}{4}$×（$\frac{1}{4}$）4 | C． | $\frac{\sqrt{3}}{8}$×（$\frac{1}{4}$）5 | D． | $\frac{\sqrt{3}}{4}$×（$\frac{1}{4}$）5 |
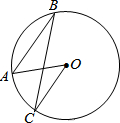已知，点A、B、C为⊙O上的点，若∠C=15°，且AB∥OC，则∠A的度数为30°．