题目内容
14.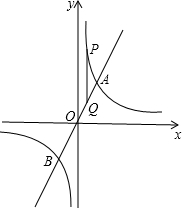 如图,已知直线y=kx(k>0)与双曲线y=$\frac{8}{x}$交于A、B两点,且点A的纵坐标为4,第一象限的双曲线上有一点P(1,a),过点P作PQ∥y轴交直线AB于点Q.
如图,已知直线y=kx(k>0)与双曲线y=$\frac{8}{x}$交于A、B两点,且点A的纵坐标为4,第一象限的双曲线上有一点P(1,a),过点P作PQ∥y轴交直线AB于点Q.(1)直接写出k的值及点B的坐标;
(2)求线段PQ的长;
(3)如果在直线y=kx上有一点M,且满足△BPM的面积等于12,求点M的坐标.
分析 (1)先求得A点坐标,再代入直线解析式可求得k的值,根据对称性可求得B点坐标;
(2)由反比例函数解析式可求得P点坐标,由直线解析式可求得Q点坐标,可求得PQ的长;
(3)可设M坐标为(m,2m),分点M在线段BQ的延长线上和线段QB的延长线上两种情况,分别表示出△BPM的面积,可求得m的值,可求得M的坐标.
解答 解:(1)∵A在双曲线y=$\frac{8}{x}$交于,且A的纵坐标为4,
∴A坐标为(2,4),
代入直线y=kx,可得4=2k,解得k=2,
又A、B关于原点对称,
∴点B的坐标为(-2,-4).
(2)∵点P(1,a)在双曲线上,
∴代入$y=\frac{8}{x}$,可得点P的坐标为(1,8).
∵PQ∥y轴,且点Q在直线AB上,
∴可设点Q的坐标为(1,b).
代入y=2x,得点Q的坐标为(1,2).
∴PQ=6.
(3)设点M的坐标为(m,2m).
S△BPQ=$\frac{1}{2}×6×3=9$.
①当点M在BQ的延长线上时,S△BPM=S△BPQ+S△MPQ,$12=9+\frac{1}{2}×6×(m-1)$,m=2.
点M的坐标为(2,4).
②当点M在QB的延长线上时,S△BPM=S△MPQ-S△BPQ,$12=\frac{1}{2}×6×(1-m)-9$,m=-6.
点M的坐标为(-6,-12).
综上所述:点M的坐标为(2,4),(-6,-12).
点评 本题主要考查函数的交点问题,掌握函数图象的交点坐标满足每个函数的解析式是解题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
5.一项工程由甲工程队单独完成需要12天,由乙工程队单独完成需要16天,甲工程队单独施工5天后,为加快工程进度,又抽调乙工程队加入该工程施工,问还需多少天可以完成该工程?如果设还需x天可以完成该工程,则可列方程为( )
| A. | $\frac{5+x}{12}+\frac{x}{16}=1$ | B. | $\frac{x}{12}+\frac{5+x}{16}=1$ | C. | 12(5+x)+16x=1 | D. | 12(5+x)=16x |
9.函数y=kx与y=-$\frac{k}{x}$在同一坐标系内的大致图象是( )
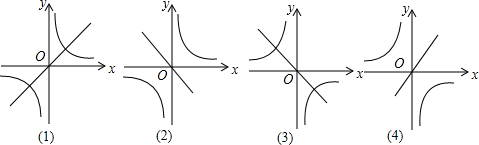

| A. | (1)和(2) | B. | (1)和(3) | C. | (2)和(3) | D. | (2)和(4) |
6.能用平方差公式进行计算的是( )
| A. | (2a-b)(-b+2a) | B. | (a-2b)(2a+b) | C. | (-2a-b)(2a+b) | D. | (-2a-b)(-2a+b) |
4.在二次函数y=(x-1)2-1中,常数项是( )
| A. | 1 | B. | -1 | C. | 0 | D. | -2 |