题目内容
3.解下列一元二次方程:(1)(x-3)2=16;
(2)(x-3)(x+1)=1
(3)4x2-9=4x-6;
(4)3(x+5)2=x2-25.
分析 (1)根据完全平方式对原方程进行开平方得到x-3=±4,然后求得方程的根;
(2)对原方程进行化简得到x2-2x-4=0,然后利用配方法求得方程的根;
(3)将原方程化简为4x2-4x-3=0,然后利用因式分解法求得方程的根;
(4)利用因式分解法求得方程的根.
解答 解:(1)∵(x-3)2=16,
∴x-3=±4,
∴x=3±4,
∴x1=-1,x2=7;
(2)∵(x-3)(x+1)=1,
∴x2-2x-4=0,
∴(x-1)2=5,
x-1=±$\sqrt{5}$,
x1=1+$\sqrt{5}$,x2=1-$\sqrt{5}$;
(3)∵4x2-9=4x-6,
∴4x2-4x-3=0,
∴(2x-3)(2x+1)=0,
2x-3=0,2x+1=0,
∴x1=$\frac{3}{2}$,x2=-$\frac{1}{2}$;
(4)∵3(x+5)2=x2-25,
∴3(x+5)2=(x-5)(x+5),
∴(x+5)(3x+15-x+5)=0,
∴x+5=0或2x+20=0,
∴x1=-5,x2=-10.
点评 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.小彭同时投掷两枚普通的正方体骰子(骰子各个面分别标有点数1,2,3,4,5,6),所得两个数字之和小于4的概率是( )
| A. | $\frac{1}{12}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{4}$ |
15.甲队修路120m与乙队修路100m所用的天数相同,已知甲队比乙队每天多修10m,则甲队每天修路( )
| A. | 50m | B. | 60m | C. | 70m | D. | 80m |
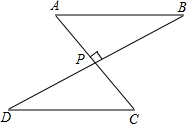 如图,AC⊥BD于P,AP=CP,增加下列一个条件:(1)BP=DP;(2)AB=CD;(3)∠A=∠C,其中能判定△ABP≌△CDP的条件有( )
如图,AC⊥BD于P,AP=CP,增加下列一个条件:(1)BP=DP;(2)AB=CD;(3)∠A=∠C,其中能判定△ABP≌△CDP的条件有( )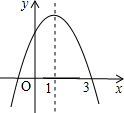 已知二次函数y=ax2+bx+c的图象如图所示,对称轴为x=1,下列结论:
已知二次函数y=ax2+bx+c的图象如图所示,对称轴为x=1,下列结论: