题目内容
13.已知n为正奇数,则式子(n+11)2-(n+1)2一定能被20整除.分析 用平方差公式展开(n+11)2-(n+1)2,根据因式中的因数进行填空.
解答 解:(n+11)2-(n+1)2
=(n+11+n+1)(n+11-n-1),
=20(n+6).
因为n是正奇数,所以(n+6)是正奇数,
故20(n+6)即(n+11)2-(n+1)2一定能被20整除.
故答案是:20.
点评 主要考查利用平方差公式分解因式.公式:a2-b2=(a+b)(a-b).

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
3.(-3)2的平方根是( )
| A. | 3 | B. | -3 | C. | ±3 | D. | 9 |
4.下列说法正确的是( )
| A. | $\frac{π}{2}$是分数 | B. | $\sqrt{(-2)^{2}}$是负数 | C. | $\sqrt{0.9}$是有理数 | D. | $\root{3}{0.01}$是无理数 |
2.某中学为丰富学生的校园生活,准备从商店购买若干个足球和篮球,已知购买2个足球和4个篮球需420元,购买3个足球比1个篮球要多花70元.
(1)购买一个足球、一个篮球各需多少元?
(2)若学校准备用不超过1600元购买足球和篮球两种球共30个,则学校有哪几种购买方案?
(3)在”五一“期间,该商店对足球、篮球这两种商品进行如下优惠促销活动:
按上述优惠条件,七年级(1)班第一天购买足球一次性付款200元,第二天值购买篮球打折后一次性付款360元,求该班购买足球、篮球各多少个?而(2)班一次性购买这两种球,同样也是花560元,求该班购买足球、篮球各多少个?
(1)购买一个足球、一个篮球各需多少元?
(2)若学校准备用不超过1600元购买足球和篮球两种球共30个,则学校有哪几种购买方案?
(3)在”五一“期间,该商店对足球、篮球这两种商品进行如下优惠促销活动:
| 一次性购买的总金额 | 优惠措施 |
| 不超过300元 | 不优惠 |
| 超过300元且不超过500元 | 售价打九折 |
| 超过500元 | 售价打八折 |
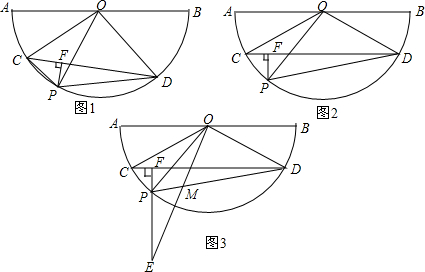
 如图,四边形ABCD中,∠A=∠C.若BE,DF分别是∠ABC,∠ADC的平分线,问DF与BE的位置关系,并证明.
如图,四边形ABCD中,∠A=∠C.若BE,DF分别是∠ABC,∠ADC的平分线,问DF与BE的位置关系,并证明.