题目内容
4. 如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=12cm,BC=18cm,点P从点A出发以2cm/s的速度沿A→D→C运动,点P从点A出发1秒后,点Q从点C出发,并以1cm/s速度向点B运动,当点P到达点C时,点Q也停止运动.设点P的运动时间为t秒.
如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=12cm,BC=18cm,点P从点A出发以2cm/s的速度沿A→D→C运动,点P从点A出发1秒后,点Q从点C出发,并以1cm/s速度向点B运动,当点P到达点C时,点Q也停止运动.设点P的运动时间为t秒.(1)求DC的长;
(2)当t取何值时,PQ∥CD?
(3)是否存在t,使△PQC为直角三角形?
分析 (1)过D点作DF⊥BC于F,得出四边形ABFD是矩形,那么DF=AB=8,BF=AD=12,CF=BC-BF=6,然后在直角△CDF中利用勾股定理即可求出DC;
(2)由于AD∥BC,所以当PQ∥CD时,四边形PDCQ是平行四边形,根据平行四边形的对边相等得出PD=QC,依此列出关于t的方程,求解即可;
(3)因为∠C<90°,所以△PQC为直角三角形时,分两种情况:①∠PQC=90°;②∠CPQ=90°;分别求解即可.
解答  解:(1)过D点作DF⊥BC于F,
解:(1)过D点作DF⊥BC于F,
∵AD∥BC,∠B=90°,
∴四边形ABFD是矩形,
∴DF=AB=8,BF=AD=12,
∴CF=BC-BF=18-12=6,
∴DC=$\sqrt{D{F}^{2}+C{F}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10(cm); (2)当PQ∥CD时,四边形PDCQ是平行四边形,此时PD=QC,
(2)当PQ∥CD时,四边形PDCQ是平行四边形,此时PD=QC,
∴12-2t=t-1,
∴t=4$\frac{1}{3}$.
∴当t=4$\frac{1}{3}$时,四边形PQDC是平行四边形;
(3)△PQC为直角三角形时,因为∠C<90°,分两种情况:
①当∠PQC=90°时,则AP=BQ, 即2t=18-(t-1),
即2t=18-(t-1),
解得t=6$\frac{1}{3}$,不合题意舍去;
②当∠CPQ=90°,此时P一定在DC上,
∵CP=10+12-2t=22-2t,CQ=t-1,
易知,△CDF∽△CQP,
∴$\frac{CF}{CP}$=$\frac{CD}{CQ}$,即$\frac{6}{22-2t}$=$\frac{10}{t-1}$,
解得:t=8$\frac{9}{13}$,符合题意;
综上所述,当t=8$\frac{9}{13}$秒时,△PQC是直角三角形.
点评 此题是四边形综合题,考查了平行四边形、矩形、相似三角形的判定与性质,勾股定理,直角三角形的性质等知识,综合性较强,难度适中.利用分类讨论和数形结合是解题的关键.

 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案 在平面直角坐标系xOy中,抛物线y=ax2+bx经过点A(-3,4),直线l与x轴相交于点B,与∠AOB的平分线相交于点C,直线l的解析式为y=kx-5k(k≠0),BC=OB.
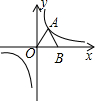
在平面直角坐标系xOy中,抛物线y=ax2+bx经过点A(-3,4),直线l与x轴相交于点B,与∠AOB的平分线相交于点C,直线l的解析式为y=kx-5k(k≠0),BC=OB. 如图,已知直线y=3x-3分别交x轴、y轴于A、B两点,抛物线y=x2+bx+c经过A、B两点,点C是抛物线与x轴的另一个交点,该抛物线的对称轴与x轴交于点E.
如图,已知直线y=3x-3分别交x轴、y轴于A、B两点,抛物线y=x2+bx+c经过A、B两点,点C是抛物线与x轴的另一个交点,该抛物线的对称轴与x轴交于点E.
 如图,等边△OAB的边长为2,点B在x轴上,点A在双曲线y=$\frac{k}{x}$(k≠0)上,将△OAB绕点O顺时针旋转α度(0<α<360°),使点A仍落在双曲线y=$\frac{k}{x}$(k≠0)上,则α的值不可能是( )
如图,等边△OAB的边长为2,点B在x轴上,点A在双曲线y=$\frac{k}{x}$(k≠0)上,将△OAB绕点O顺时针旋转α度(0<α<360°),使点A仍落在双曲线y=$\frac{k}{x}$(k≠0)上,则α的值不可能是( )