题目内容
17.数学规律在数学中有着极其重要的意义,我们要善于抓住主要矛盾,提炼出我们需要的信息,从而解决问题.(1)观察下列算式:31=3,32=9,33=27,34=81,35=243,36=729,37=2187,38=6561,…,
通过观察,用你所发现的规律确定32014的个位数字是9
(2)观察一列数2,4,8,16,32,…,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是2;根据此规律,如果an(n为正整数)表示这个数列的第n项,那么a18=218,an=2n;
(3)观察下面的一列单项式:x,-2x2,4x3,-8x4,…根据你发现的规律,第7个单项式为64x7;第n个单项式为(-1)n-12n-1xn.
分析 (1)个位数字以3、9、7、1四个数字一循环,用2014除以4,余数是2就和第2个个位数字数字相同,由此解决问题即可
(2)从第二项开始,每一项与前一项之比是2;有第一个数为2,故可得a18,an的值;
(3)奇数项符号为正,偶数项符号为负,数字变化规律是2n-1,字母变化规律是xn.
解答 解:(1)末位数字以3、9、7、1四个数字为一循环,
又2014÷4=503…2,
所以32014的末位数字与32的末位数字相同是9;
(2)每一项与前一项之比是一个常数,这个常数是2,a18=218,an=2n;
(3)第7个单项式为(-1)7-127-1x7,即64x7.第n个单项式是(-1)n-12n-1xn.
故答案为:9;2,218,2n;64x7,(-1)n-12n-1xn.
点评 此题考查数字的变化规律,找出数字的运算规律与循环规律,利用规律解决问题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
5.2014年西安城墙国际马拉松赛已于11月1日上午9:00在西安城墙南门上举行,所有参赛选手要跑完全程,约为13.7千米.那么13.7千米用科学记数法可表示为( )
| A. | 1.37×103米 | B. | 13.7×103米 | C. | 1.37×104米 | D. | 13.7×102米 |
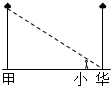 如图,甲、乙两盏路灯底部间的距离是25米,一天晚上,当小华走到距路灯乙底部4米处时,发现自己的身影顶部正好接触路灯乙的底部.已知小华的身高为1.6米,那么路灯甲的高为10米.
如图,甲、乙两盏路灯底部间的距离是25米,一天晚上,当小华走到距路灯乙底部4米处时,发现自己的身影顶部正好接触路灯乙的底部.已知小华的身高为1.6米,那么路灯甲的高为10米. 如图,在数轴上有O,A,B,C,D五点,根据图中各点所表示的数,判断$\sqrt{18}$在数轴上的位置会落在线段BC上.
如图,在数轴上有O,A,B,C,D五点,根据图中各点所表示的数,判断$\sqrt{18}$在数轴上的位置会落在线段BC上.