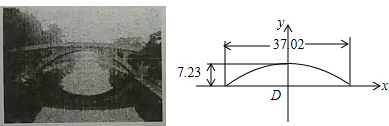
题目内容
11.已知|a-1|+|b+3|=0,求b-a+$\frac{1}{2}$的值.分析 根据非负数的性质求得a、b的值,然后代入计算即可.
解答 解:∵|a-1|+|b+3|=0,
∴a=1,b=-3.
将a=1,b=-3代入得:b-a+$\frac{1}{2}$=-3-1+$\frac{1}{2}$=-3$\frac{1}{2}$.
点评 本题主要考查的是求代数式的值,利用非负数的性质求得a、b的值是解题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
19.关于x的一元二次方程mx2+(2m-1)x-2=0的根的判别式等于4,则m的值是( )
| A. | $\frac{1}{2}$ | B. | $-\frac{3}{2}$ | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$或$-\frac{3}{2}$ |
16.下列说法正确的是( )
| A. | 零是正数不是负数 | B. | 零既不是正数也不是负数 | ||
| C. | 零既是正数也是负数 | D. | 正数,负数和零统称有理数 |
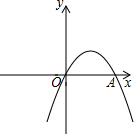 如图,抛物线y=-x2+bx+c经过坐标原点,并与x轴相交于点A(2,0).
如图,抛物线y=-x2+bx+c经过坐标原点,并与x轴相交于点A(2,0).