题目内容
已知△ABC中，∠A：∠B：∠C=1：3：5，求∠A、∠B和∠C的度数，它是什么三角形？
考点：三角形内角和定理
专题：
分析：设∠A=x，则∠B=3x，∠C=5x，再根据三角形内角和定理求出x的度数，进而可得出结论．
解答：解：∵△ABC中∠A：∠B：∠C=1：3：5，
∴设∠A=x，则∠B=3x，∠C=5x，
∴∠A+∠B+∠C=180°，即x+3x+5x=180°，解得x=20°，
∴∠A=20°，∠B=60°，∠C=100°，
∴△ABC是钝角三角形．
∴设∠A=x，则∠B=3x，∠C=5x，
∴∠A+∠B+∠C=180°，即x+3x+5x=180°，解得x=20°，
∴∠A=20°，∠B=60°，∠C=100°，
∴△ABC是钝角三角形．
点评：本题考查的是三角形内角和定理，熟知三角形内角和是180°是解答此题的关键．
练习册系列答案
相关题目
对于正数x，规定 f(x)=
，例如：f(4)=
=
，f(
)=
=
，则f(2013)+f(2012)+…+f(2)+f(1)+f(
)+f(
)+…+f(
)的值为（ ）
| 1 |
| 1+x |
| 1 |
| 1+4 |
| 1 |
| 5 |
| 1 |
| 4 |
| 1 | ||
1+
|
| 4 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2013 |
| A、2012 |
| B、2012.5 |
| C、2013 |
| D、2013.5 |
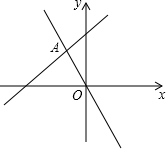如图，函数y=-2x和y=kx+b的图象相交于点A（m，3），则关于x的不等式kx+b+2x＞0的解集为（ ）A、x＞
| ||
| B、x＜m | ||
| C、x＞m | ||
D、x＞-
|