题目内容
20.请证明:五边形的内角和为540o.(要求:画出图形,写出已知,求证,证明)分析 因为过五边形的一个顶点可做2条对角线,即可以把五边形分成3个三角形.已知三角形的内角和是180°,那么3×180°=540°.所以五边形的内角和得以证明.
解答 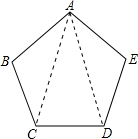 解:已知:如图,五边形 ABCDE.
解:已知:如图,五边形 ABCDE.
求证:∠A+∠B+∠C+∠D+∠E=540°.
证明:如图,五边形 ABCDE,连接 AC,连接 AD,
形成三个三角形:△ABC,△ACD,△ADE,
∵∠A+∠B+∠C+∠D+∠E=∠BAC+∠B+∠BCA+∠CAD+∠ACD+∠ADC+DAE+∠ADE+∠E,
由于三角形内角和是 180°,
∴∠BAC+∠B+∠BCA=180°,∠CAD+∠ACD+∠ADC=180°,DAE+∠ADE+∠E=180°,
∴∠A+∠B+∠C+∠D+∠E=180°×3=540°,
所以五边形 ABCDE 的内角和等于 180°×3=540°.
点评 本题考查了五边形内角和的证明.从具体的简单的问题入手常能找到解决问题的思路,本题通过将五边形分割为三角形的方法简单易行.

练习册系列答案
相关题目

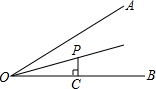 如图,∠AOB=30°,OP平分∠AOB,PC⊥OB于点C,若OC=1,则PC的长是2-$\sqrt{3}$.
如图,∠AOB=30°,OP平分∠AOB,PC⊥OB于点C,若OC=1,则PC的长是2-$\sqrt{3}$. 如图,抛物线y1=a(x-h)2与直线y2=kx+b交于A(0,-1),B(1,0)两点.
如图,抛物线y1=a(x-h)2与直线y2=kx+b交于A(0,-1),B(1,0)两点.