题目内容
已知x轴上的点A(2n-4,n+1)和y轴上的点B(3m-6,m+2),及坐标轴上的一点C,构成的△ABC的面积是16,求点C坐标.
考点:坐标与图形性质,三角形的面积
专题:
分析:根据x轴上点的纵坐标为0列式求出n,y轴上的点的横坐标为0列式求出m,从而得到点A、B的坐标,再分点C在x轴上求出AC,然后分两种情况求出OC,再写出点C的坐标;点C在y轴上,求出BC,然后分两种情况求出OC,再写出点C的坐标.
解答:解:∵点A(2n-4,n+1)在x轴上,点B(3m-6,m+2)在y轴上,
∴n+1=0,3m-6=0,
解得n=-1,m=2,
∴点A(-6,0),B(0,4),
①点C在x轴上时,
AC•4=16,
解得AC=8,
若点C在点A的左边,则OC=-6-8=-14,
若点C在点A的右边,则OC=-6+8=2,
此时,点C的坐标(-14,0),(2,0),
②点C在y轴上时,
BC•6=16,
解得BC=
,
若点C在点B的上边,则OC=4+
=
,
若点C在点B的下边,则OC=4-
=-
,
此时,点C的坐标(
,0),(-
,0),
综上所述,点C的坐标为(-14,0)或(2,0)或(
,0)或(-
,0).
∴n+1=0,3m-6=0,
解得n=-1,m=2,
∴点A(-6,0),B(0,4),
①点C在x轴上时,
| 1 |
| 2 |
解得AC=8,
若点C在点A的左边,则OC=-6-8=-14,
若点C在点A的右边,则OC=-6+8=2,
此时,点C的坐标(-14,0),(2,0),
②点C在y轴上时,
| 1 |
| 2 |
解得BC=
| 16 |
| 3 |
若点C在点B的上边,则OC=4+
| 16 |
| 3 |
| 28 |
| 3 |
若点C在点B的下边,则OC=4-
| 16 |
| 3 |
| 4 |
| 3 |
此时,点C的坐标(
| 28 |
| 3 |
| 4 |
| 3 |
综上所述,点C的坐标为(-14,0)或(2,0)或(
| 28 |
| 3 |
| 4 |
| 3 |
点评:本题考查了坐标与图形性质,熟记坐标轴上点的坐标特征是解题的关键,难点在于根据点C的位置分情况讨论.

练习册系列答案
相关题目
下列说法中,错误的是( )
| A、所有的等边三角形都相似 |
| B、所有的等腰直角三角形都相似 |
| C、所有的矩形都相似 |
| D、所有的正方形都相似 |
若-3xmy2与2x3yn是同类项,则m,n分别等于( )
| A、1,2 | B、3,2 |
| C、2,3 | D、2,1 |
 如图,C、D是直线l两侧的点,试在直线l上找一点Q,使|CQ-DQ|最大.
如图,C、D是直线l两侧的点,试在直线l上找一点Q,使|CQ-DQ|最大. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).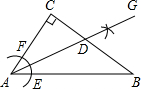 如图,在△ABC,∠C=90°,∠ABC=40°,按以下步骤作图:
如图,在△ABC,∠C=90°,∠ABC=40°,按以下步骤作图: