题目内容
在△ABC中,∠A=150°,AB=20m,AC=30m,求△ABC的面积.
考点:含30度角的直角三角形
专题:
分析:过点B作BE⊥AC,根据含30度角的直角三角形性质可求得BE,再根据三角形的面积公式求出答案.
解答:解:过点B作BE⊥AC,交CA延长线于E,则∠E=90°,
∵∠A=150°,
∴∠BAE=180°-∠BAC=180°-150°=30°,
∵在△BEA中,∠E=90°,AB=20m,
∴BE=
AB=10m,
∴S△ABC=
AC•BE=
×30m×10m=150m2,
即△ABC的面积是150m2.

∵∠A=150°,
∴∠BAE=180°-∠BAC=180°-150°=30°,
∵在△BEA中,∠E=90°,AB=20m,
∴BE=
| 1 |
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
即△ABC的面积是150m2.
点评:本题考查了含30度角的直角三角形性质和三角形的面积公式,是基础知识比较简单.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
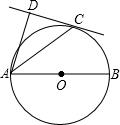 如图,AB为⊙O的直径,C为⊙O上的一点,DA和过点C的切线互相垂直,垂足为D,若∠DAB=70°,求∠DAC的度数.
如图,AB为⊙O的直径,C为⊙O上的一点,DA和过点C的切线互相垂直,垂足为D,若∠DAB=70°,求∠DAC的度数.
 如图,在平面直角坐标系中,直线y=2x-6与x轴,y轴分别相交于A,B,C在x轴上.若△ABC是等腰三角形,试求点C的坐标.
如图,在平面直角坐标系中,直线y=2x-6与x轴,y轴分别相交于A,B,C在x轴上.若△ABC是等腰三角形,试求点C的坐标.