题目内容
7. 已知反比例函数y=$\frac{6}{x}$.
已知反比例函数y=$\frac{6}{x}$.(1)若该反比例函数的图象与直线y=-x+a(a>0)有两个不同交点,求a的取值范围;
(2)如图,在(1)条件下,若直线y=-x+a(a>0)与反比例函数的图象交于A、B两点,求证:A、B关于直线y=x的对称.
分析 (1)根据题意可得$\frac{6}{x}$=-x+a,则x2-ax+6=0,利用根的判别式求解;
(2)求得反比例函数与y=-x+a组成的方程组,求得A和B的坐标即可作出判断.
解答 解:(1)根据题意得$\frac{6}{x}$=-x+a,则x2-ax+6=0,
△=a2-24>0,
解得-2$\sqrt{6}$<a<2$\sqrt{6}$,
又∵a>0,
∴a的取值范围是0<a<2$\sqrt{6}$;
(2)根据题意得$\left\{\begin{array}{l}{y=\frac{6}{x}}\\{y=-x+a}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{a+\sqrt{{a}^{2}-24}}{2}}\\{y=\frac{a-\sqrt{{a}^{2}-24}}{2}}\end{array}\right.$,$\left\{\begin{array}{l}{x=\frac{a-\sqrt{{a}^{2}-24}}{2}}\\{y=\frac{a+\sqrt{{a}^{2}-24}}{2}}\end{array}\right.$,
则A的坐标是($\frac{a+\sqrt{{a}^{2}-24}}{2}$,$\frac{a-\sqrt{{a}^{2}-24}}{2}$),B的坐标是($\frac{a-\sqrt{{a}^{2}-24}}{2}$,$\frac{a+\sqrt{{a}^{2}-24}}{2}$).
则AB关于直线y=x对称.
点评 本题考查了一次函数与反比例函数的交点坐标,正确解方程组求得A和B的坐标是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.钓鱼岛是中国的固有领土,面积约4400000平方米,数据4400000用科学记数法表示应为( )
| A. | 44×105 | B. | 0.44×107 | C. | 4.4×106 | D. | 4.4×105 |
18.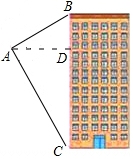 如图,热气球从空中的A处看一栋楼的顶部仰角为30°,看这栋楼的俯角为60°.热气球与楼的水平距离为120m.这栋楼的高度为( )
如图,热气球从空中的A处看一栋楼的顶部仰角为30°,看这栋楼的俯角为60°.热气球与楼的水平距离为120m.这栋楼的高度为( )
 如图,热气球从空中的A处看一栋楼的顶部仰角为30°,看这栋楼的俯角为60°.热气球与楼的水平距离为120m.这栋楼的高度为( )
如图,热气球从空中的A处看一栋楼的顶部仰角为30°,看这栋楼的俯角为60°.热气球与楼的水平距离为120m.这栋楼的高度为( )| A. | 160m | B. | 160$\sqrt{3}$m | C. | (160-160$\sqrt{3}$)m | D. | 360m |
15.不等式$\frac{x}{2}$$-\frac{x-1}{3}$≤1的解集是( )
| A. | x≥-1 | B. | x≤-1 | C. | x≥4 | D. | x≤4 |
12.下列事件:①在体育中考中,小明考了满分;②经过有交通信号灯的路口,遇到红灯;③抛掷两枚正方体骰子,点数和大于1;④度量任一三角形,其外角和都是180°,其中必然事件是( )
| A. | ① | B. | ② | C. | ③ | D. | ④ |
19.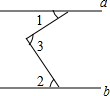 如图,已知直线a∥b,∠1=46°.∠2=66°,则∠3等于( )
如图,已知直线a∥b,∠1=46°.∠2=66°,则∠3等于( )
 如图,已知直线a∥b,∠1=46°.∠2=66°,则∠3等于( )
如图,已知直线a∥b,∠1=46°.∠2=66°,则∠3等于( )| A. | 112° | B. | 100° | C. | 130° | D. | 120° |
16. 如图,下列结论正确的个数是( )
如图,下列结论正确的个数是( )
①m+n>0;②m-n>0;③mn<0;④|m-n|=m-n.
 如图,下列结论正确的个数是( )
如图,下列结论正确的个数是( )①m+n>0;②m-n>0;③mn<0;④|m-n|=m-n.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,△ABC中,DE∥FG∥BC,AD:DF:FB=2:3:4,若EG=4,则AC=12.
如图,△ABC中,DE∥FG∥BC,AD:DF:FB=2:3:4,若EG=4,则AC=12.