题目内容
2. 如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )| A. | 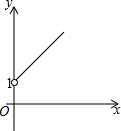 | B. | 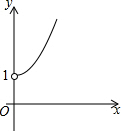 | C. | 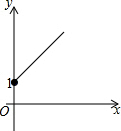 | D. | 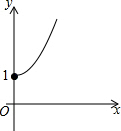 |
分析 根据题意作出合适的辅助线,可以先证明△ADC和△AOB的关系,即可建立y与x的函数关系,从而可以得到哪个选项是正确的.
解答 解:作AD∥x轴,作CD⊥AD于点D,如右图所示, 由已知可得,OB=x,OA=1,∠AOB=90°,∠BAC=90°,AB=AC,点C的纵坐标是y,
由已知可得,OB=x,OA=1,∠AOB=90°,∠BAC=90°,AB=AC,点C的纵坐标是y,
∵AD∥x轴,
∴∠DAO+∠AOD=180°,
∴∠DAO=90°,
∴∠OAB+∠BAD=∠BAD+∠DAC=90°,
∴∠OAB=∠DAC,
在△OAB和△DAC中,
$\left\{\begin{array}{l}{∠AOB=∠ADC}\\{∠OAB=∠DAC}\\{AB=AC}\end{array}\right.$,
∴△OAB≌△DAC(AAS),
∴OB=CD,
∴CD=x,
∵点C到x轴的距离为y,点D到x轴的距离等于点A到x的距离1,
∴y=x+1(x>0).
故选:A.
点评 本题考查动点问题的函数图象,解题的关键是明确题意,建立相应的函数关系式,根据函数关系式判断出正确的函数图象.

练习册系列答案
相关题目
13.五名同学参加演讲比赛,以抽签的方式决定每个人的出场顺序.把背面完全相同,正面写有1、2、3、4、5的五张卡片洗均后正面向下放在桌子上,小军从中随机抽取一张,下列事件是随机事件的是( )
| A. | 抽到的数字是0 | B. | 抽到的数字是7 | C. | 抽到的数字大于5 | D. | 抽到的数字是1 |
17.-$\frac{1}{3}$的相反数是( )
| A. | $\frac{1}{3}$ | B. | -3 | C. | 3 | D. | -$\frac{1}{3}$ |
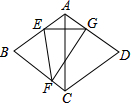 如图,在菱形ABCD中,∠BAD=120°,点E、F分别在边AB、BC上,△BEF与△GEF关于直线EF对称,点B的对称点是点G,且点G在边AD上.若EG⊥AC,AB=6$\sqrt{2}$,则FG的长为3$\sqrt{6}$.
如图,在菱形ABCD中,∠BAD=120°,点E、F分别在边AB、BC上,△BEF与△GEF关于直线EF对称,点B的对称点是点G,且点G在边AD上.若EG⊥AC,AB=6$\sqrt{2}$,则FG的长为3$\sqrt{6}$. 如图,在平面直角坐标系中,己知点A(-1,3)和点B(2,2),若四边ABCD是正方形,则点C的坐标为(2,-1)或(3,5).
如图,在平面直角坐标系中,己知点A(-1,3)和点B(2,2),若四边ABCD是正方形,则点C的坐标为(2,-1)或(3,5).