题目内容
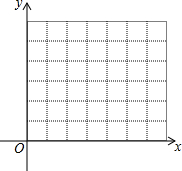 已知△A′B′C′是由△ABC是由△ABC经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:
已知△A′B′C′是由△ABC是由△ABC经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:| △ABC | A(1,1) | B(4,4) | C(3,1) |
| △A′B′C′ | A′(4,2) | B′(7,5) | C′(a,2) |
(2)在平面直角坐标系中画出△ABC及平移后的△A′B′C′;
(3)直接写出△A′B′C′的面积是
考点:作图-平移变换
专题:
分析:(1)根据图形平移的性质得出a的值即可;
(2)在坐标系内画出画出△ABC及平移后的△A1B1C1即可;
(2)根据△A′B′C′的面积等于正方形的面积减去两个顶点上三角形的面积即可得出结论.
(2)在坐标系内画出画出△ABC及平移后的△A1B1C1即可;
(2)根据△A′B′C′的面积等于正方形的面积减去两个顶点上三角形的面积即可得出结论.
解答: 解:(1)∵7-4=a-3,
解:(1)∵7-4=a-3,
∴a=6.
故答案为:6;
(2)如图所示;
(3)S△A′B′C′=3×3-
×3×3-
×3×1=3.
故答案为:3.
 解:(1)∵7-4=a-3,
解:(1)∵7-4=a-3,∴a=6.
故答案为:6;
(2)如图所示;
(3)S△A′B′C′=3×3-
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:3.
点评:本题考查的是作图-平移变换,熟知图形平移不变性的性质是解答此题的关键.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 如图,H、Q分别是正方形ABCD的边AB、BC上的点,且BH=BQ,过B作HC的垂线,垂足为P.求证:DP⊥PQ.
如图,H、Q分别是正方形ABCD的边AB、BC上的点,且BH=BQ,过B作HC的垂线,垂足为P.求证:DP⊥PQ. 在如图10×10的网格中,每个小方格都是边长为1个单位长度的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).
在如图10×10的网格中,每个小方格都是边长为1个单位长度的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).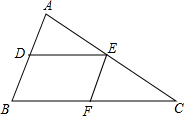 如图,已知DE∥BC,EF∥AB,从下列选项中选择一个正确的并说明理由.
如图,已知DE∥BC,EF∥AB,从下列选项中选择一个正确的并说明理由.