题目内容
如图，在梯形ABCD中，AD∥BC，EF是中位线，AF平分∠BAD．求证：AB=2EF．考点：梯形中位线定理
专题：证明题
分析：根据中位线的性质和和角平分线的性质得到∠EFA=∠EAF，从而利用等角对等边得到EF=AE，从而得解．
解答：证明：∵AF平分∠BAD，
∴∠BAF=∠DAF，
∵EF是中位线，
∴EF∥AD，
∴∠EFA=∠FAD，
∴∠EFA=∠EAF，
∴EF=AE，
∵AB=2AE，
∴AB=2EF．
∴∠BAF=∠DAF，
∵EF是中位线，
∴EF∥AD，
∴∠EFA=∠FAD，
∴∠EFA=∠EAF，
∴EF=AE，
∵AB=2AE，
∴AB=2EF．
点评：本题考查了梯形的中位线定理，解题的关键是能够利用梯形的中位线的位置关系得到平行，从而为证明两角相等奠定基础．
练习册系列答案
巧学巧练系列答案
相关题目
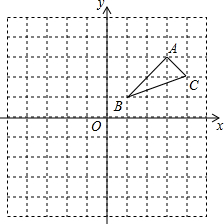在如图10×10的网格中，每个小方格都是边长为1个单位长度的正方形，△ABC的三个顶点都在格点上（每个小方格的顶点叫格点）．
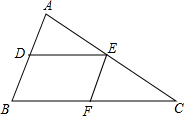如图，已知DE∥BC，EF∥AB，从下列选项中选择一个正确的并说明理由．
已知一次函数的图象经过（6，-3）和（-3，6）两点，