题目内容
14. 先阅读,然后回答问题:
先阅读,然后回答问题:化简:$\sqrt{{x}^{2}-6x+9}+\sqrt{{x}^{2}+4x+4}$.
由于题中没有给出x的取值范围,所以要先分类讨论.
$\sqrt{{x}^{2}-6x+9}+\sqrt{{x}^{2}+4x+4}$
=$\sqrt{(x-3)^{2}}+\sqrt{(x+2)^{2}}$
=|x-3|+|x+2|.
令x-3=0,x+2=0,分别求出x=3,x=-2(称3,-2分别为$\sqrt{(x-3)^{2}},\sqrt{(x+2)^{2}}$的零点值),然后在数轴上标出表示3和-2的点,如图所示,数轴被分成三段,即x<-2,-2≤x<3,x≥3.
当x<-2时,原式=-(x-3)-(x+2)=-x+3-x-2=-2x+1;
当-2≤x<3时,原式=-(x-3)+(x+2)=-x+3+x+2=5;
当x≥3时,原式=(x-3)+(x+2)=x-3+x+2=2x-1.
(1)分别求出$\sqrt{(x+1)^{2}}$和$\sqrt{(x-2)^{2}}$的零点值;
(2)化简:$\sqrt{{x}^{2}+2x+1}+\sqrt{{x}^{2}-4x+4}$.
分析 (1)令x+1=0,x-2=0,求出x的值即可.
(2)根据题意给出方法即可求出答案.
解答 解:(1)令x+1=0,
∴x=-1
令x-2=0
∴x=2
∴$\sqrt{(x+1)^{2}}$与$\sqrt{(x-2)^{2}}$的零点值为-1与2
(2)原式=$\sqrt{(x+1)^{2}}$+$\sqrt{(x-2)^{2}}$
=|x+1|+|x-2|
当x≤-1时,
∴x+1≤0,x-2≤-3
∴原式=-(x+1)-(x-2)
=-x-1-x+2
=-2x+1
当-1<x<2时,
∴x+1>0,x-2<0
∴原式=x+1-(x-2)
=3
当x≥2时,
∴x+1≥3,x-2≥0,
∴原式=x+1+x-2
=2x-1
点评 本题考查二次根式的性质,解题的关键是熟练运用二次根式的运算法则,本题属于基础题型.

练习册系列答案
相关题目
5.下列从左到右变形正确的是( )
| A. | -$\frac{x+1}{x-y}$=$\frac{-x+1}{x-y}$ | B. | $\frac{{x}^{2}+{y}^{2}}{x+y}$=x+y | ||
| C. | $\frac{0.5a+b}{0.2a-0.3b}$=$\frac{5a+10b}{2a-3b}$ | D. | $\frac{a-b}{a+b}$=$\frac{b-a}{b+a}$ |
2.泉州市某校准备组织教师、学生、家长到福州进行参观学习活动,旅行社代办购买动车票,动车票价格如表所示:
根据报名总人数,若所有人员都买一等座的动车票,则共需13650元;若都买二等座动车票,则共需8820元.已知家长人数是教师人数的2倍.
(1)设参加活动的老师有m人,请直接用含m的代数式表示:教师和家长都购买一等动车票所需的总费用;
(2)求参加活动的教师、家长、学生各有多少人?
(3)如果二等座动车票共买到x张,其中学生全部购买二等座动车票,剩余的人员买一等座动车票,且买票的总费用不低于9000元,求x的最大值.
| 运行区间 | 大人票价 | 学生票价 | |||
| 出发站 | 终点站 | 一等座 | 二等座 | 一等座 | 二等座 |
| 泉州 | 福州 | 65(元) | 54(元) | 65(元) | 40(元) |
(1)设参加活动的老师有m人,请直接用含m的代数式表示:教师和家长都购买一等动车票所需的总费用;
(2)求参加活动的教师、家长、学生各有多少人?
(3)如果二等座动车票共买到x张,其中学生全部购买二等座动车票,剩余的人员买一等座动车票,且买票的总费用不低于9000元,求x的最大值.
6.如果A、B都是关于x的单项式,且A•B是一个七次单项式,A+B是一个四次多项式,那么A-B的次数( )
| A. | 一定是七次 | B. | 一定是四次 | C. | 一定是三次 | D. | 无法确定 |
4.如图是若干个相同的小正方体组成的一个几何体的三视图,则小正方体的个数是( )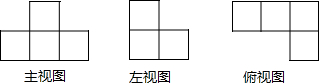

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
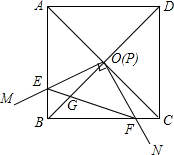 如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,∠MPN为直角,使点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM,PN分别交AB,BC于E,F两点,连接EF交OB于点G,则下列结论:①EF=$\sqrt{2}$OE;②S四边形OEBF:S正方形ABCD=1:4;③BE+BF=$\sqrt{2}$OA;④在旋转过程中,当△BEF与△COF的面积之和最大时,AE=$\frac{3}{4}$;⑤OG•BD=AE2+CF2.其中结论正确的个数是( )
如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,∠MPN为直角,使点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM,PN分别交AB,BC于E,F两点,连接EF交OB于点G,则下列结论:①EF=$\sqrt{2}$OE;②S四边形OEBF:S正方形ABCD=1:4;③BE+BF=$\sqrt{2}$OA;④在旋转过程中,当△BEF与△COF的面积之和最大时,AE=$\frac{3}{4}$;⑤OG•BD=AE2+CF2.其中结论正确的个数是( )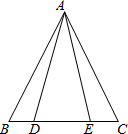 阅读并填空:如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE,试说明BD=CE的理由.
阅读并填空:如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE,试说明BD=CE的理由.