题目内容
一农妇在市场卖葱,当时市场上的葱价是1.00元一斤,一葱贩对农妇说:“我想把你的葱分开来买,葱叶0.50元一斤,葱白0.50元一斤.”农妇听了葱贩的话,不假思索就把葱全部卖完.当农妇数过钱之后才发现只卖了一半钱.此时葱贩已不见踪影.聪明的你,请运用数学语言揭穿葱贩的把戏.
过程如下:设总量z斤,葱叶x斤,葱白y斤,列方程
∵x+y=z,∴卖给葱贩的钱为0.5x+0.5y=0.5z,
而实际应卖的钱为1.0x+1.0y=1.0z,结果一目了然,那葱贩只用了一半钱就买了所有葱.
(1)生活常识告诉我们,人们在吃葱的时候主要吃的是葱白,葱白应比葱叶卖的贵.
假设一根葱的葱叶和葱白重量相同,葱叶和葱白的价钱之和仍是1.00元.请用数学语言说明此时农妇还是只卖了一半的钱.
(2)假设一根葱的葱叶和葱白重量不同,且葱叶的重量大于葱白的重量,葱叶0.20元一斤,葱白0.80元一斤.请用数学语言说明此时农妇卖的钱少于一半.
过程如下:设总量z斤,葱叶x斤,葱白y斤,列方程
∵x+y=z,∴卖给葱贩的钱为0.5x+0.5y=0.5z,
而实际应卖的钱为1.0x+1.0y=1.0z,结果一目了然,那葱贩只用了一半钱就买了所有葱.
(1)生活常识告诉我们,人们在吃葱的时候主要吃的是葱白,葱白应比葱叶卖的贵.
假设一根葱的葱叶和葱白重量相同,葱叶和葱白的价钱之和仍是1.00元.请用数学语言说明此时农妇还是只卖了一半的钱.
(2)假设一根葱的葱叶和葱白重量不同,且葱叶的重量大于葱白的重量,葱叶0.20元一斤,葱白0.80元一斤.请用数学语言说明此时农妇卖的钱少于一半.
考点:三元一次方程组的应用
专题:
分析:(1)设总量z斤,葱叶x斤,葱白y斤,由葱叶和葱白重量相同,分别表示出卖给葱贩的钱和实际应卖的钱比较即可;
(2)由葱叶的重量大于葱白的重量,分别表示出卖给葱贩的钱和实际应卖的钱比较即可.
(2)由葱叶的重量大于葱白的重量,分别表示出卖给葱贩的钱和实际应卖的钱比较即可.
解答:解:(1)设总量z斤,葱叶x斤,葱白x斤,葱叶每斤a元,葱白每斤b元
∵x+x=z,a+b=1
∴卖给葱贩的钱为ax+bx=(a+b)x=x=0.5z,
而实际应卖的钱为1.0x+1.0x=1.0z,故农妇还会少卖一半的钱;
(2)设总量z斤,葱叶x斤,葱白y斤,
∵x+y=z,0<y<x,
∴0.3x-0.3y>0
∴卖给葱贩的钱为0.2x+0.8y<0.2x+0.8y+0.3x-0.3y=0.5x+0.5y=0.5z,
而实际应卖的钱为1.0x+1.0y=1.0z,
故农妇少卖的钱少于一半.
∵x+x=z,a+b=1
∴卖给葱贩的钱为ax+bx=(a+b)x=x=0.5z,
而实际应卖的钱为1.0x+1.0x=1.0z,故农妇还会少卖一半的钱;
(2)设总量z斤,葱叶x斤,葱白y斤,
∵x+y=z,0<y<x,
∴0.3x-0.3y>0
∴卖给葱贩的钱为0.2x+0.8y<0.2x+0.8y+0.3x-0.3y=0.5x+0.5y=0.5z,
而实际应卖的钱为1.0x+1.0y=1.0z,
故农妇少卖的钱少于一半.
点评:此题考查代数式的运用,注意理解题意,列出代数式,根据不同的数值,确定代数式的大小.

练习册系列答案
相关题目
在同一坐标系中,函数y=
和y=kx+3(k≠0)的图象大致是( )
| k |
| x |
A、 |
B、 |
C、 |
D、 |
为了求1+2+22+23+…+22014的值,可令S=1+2+22+23+…+22014,则2S=2+22+23+24+…+22015,因此2S-S=22015-1,所以1+2+22+23+…+22014=22015-1.仿照以上推理计算出1+5+52+53+…+52014的值是( )
| A、52015-1 | ||
| B、52016-1 | ||
C、
| ||
D、
|
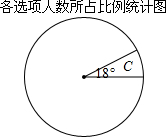 (1)在一次考试中,李老师从所教两个班全体参加考试的80名学生中随机抽取了20名学生的答题卷进行统计分析.其中某个单项选择题答题情况如下表(没有多选和不选):
(1)在一次考试中,李老师从所教两个班全体参加考试的80名学生中随机抽取了20名学生的答题卷进行统计分析.其中某个单项选择题答题情况如下表(没有多选和不选):