题目内容
16.$\frac{\sqrt{{a}^{2}}}{a}$+$\frac{b}{\sqrt{{b}^{2}}}$的值可能为0或±2.分析 根据二次根式的性质化简得到原式=$\frac{|a|}{a}$+$\frac{b}{|b|}$,然后讨论a、b的正负确定原式的值.
解答 解:原式=$\frac{|a|}{a}$+$\frac{b}{|b|}$,
当a>0,b>0,所以原式=1+1=2;
当a<0,b<0,所以原式=-1-1=-2;
当a>0,b<0,所以原式=1-1=0;
当a<0,b>0,所以原式=-1+1=0,
即原式的值为0或±2.
故答案为0或±2.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.在△ABC中,已知∠A,∠B都是锐角,且sinA=$\frac{1}{2}$,tanB=1,则∠C的度数为( )
| A. | 75° | B. | 105° | C. | 60° | D. | 45° |
1.已知等式ax+c=ay+c,则下列等式不一定成立的是( )
| A. | ax=ay | B. | x=y | C. | m-ax=m-ay | D. | 2ax=2ay |
6.下列解方程正确的是( )
| A. | 由$\frac{1}{2}$x=1,得x=$\frac{1}{2}$ | B. | 由$\frac{1}{6}$x=2,得x=3 | ||
| C. | 由-$\frac{1}{10}$x=10,得x=-100 | D. | 由-7x=1,得x=7 |
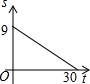 由于植被遭遇到严重破坏,某地的土地每年以相同的速度沙化,设t年后该地剩余绿地面积为S万公顷的图象如图所示,则土地沙化的速度为$\frac{3}{10}$万公顷/年,经过30年,该地的土地将全部沙化.
由于植被遭遇到严重破坏,某地的土地每年以相同的速度沙化,设t年后该地剩余绿地面积为S万公顷的图象如图所示,则土地沙化的速度为$\frac{3}{10}$万公顷/年,经过30年,该地的土地将全部沙化.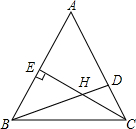 △ABC中,∠A:∠ABC:∠ACB=3:4:5,CE是AB上的高,∠BHC=135°,求证:BD⊥AC.
△ABC中,∠A:∠ABC:∠ACB=3:4:5,CE是AB上的高,∠BHC=135°,求证:BD⊥AC.